
| A. | $4\sqrt{3}$ | B. | 6 | C. | 8 | D. | 16 |
分析 先根据抛物线方程求出焦点坐标和准线方程,根据直线AF的斜率得到AF方程,与准线方程联立,解出A点坐标,因为PA垂直准线l,所以P点与A点纵坐标相同,再代入抛物线方程求P点横坐标,利用抛物线的定义就可求出|PF|长.
解答 解:∵抛物线方程为y2=8x,
∴焦点F(2,0),准线l方程为x=-2,
∵直线AF的斜率为$-\sqrt{3}$,直线AF的方程为y=$-\sqrt{3}$(x-2),
由$\left\{\begin{array}{l}{x=-2}\\{y=-\sqrt{3}(x-2)}\end{array}\right.$,可得A点坐标为(-2,4$\sqrt{3}$),
∵PA⊥l,A为垂足,
∴P点纵坐标为4$\sqrt{3}$,代入抛物线方程,得P点坐标为(6,4$\sqrt{3}$),
∴|PF|=|PA|=6-(-2)=8,
故选C.
点评 本题主要考查抛物线的几何性质,定义的应用,以及曲线交点的求法,属于综合题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d<0 | B. | d>0 | C. | a16<0 | D. | a16>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
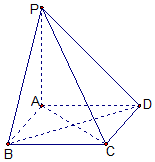 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-CD-B余弦值的大小.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-CD-B余弦值的大小.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:选择题
下列函数在其定义域内既是奇函数又是增函数的是( )
A.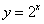 B.
B.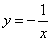
C.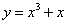 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com