
【题目】在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在棱
分别在棱![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
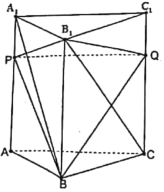
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)要证![]() 平面
平面![]() ,只需证
,只需证![]() 垂直于该面中的两条相交直线即可,通过三角形的相似,和线面垂直可证得
垂直于该面中的两条相交直线即可,通过三角形的相似,和线面垂直可证得![]() ,
,![]() ,从而可证得线面垂直;
,从而可证得线面垂直;
(2) 要求出直线![]() 与平面
与平面![]() 所成角的正弦值,关键在于需求出点
所成角的正弦值,关键在于需求出点![]() 到平面
到平面![]() 的距离,运用三棱锥的等积法
的距离,运用三棱锥的等积法![]() ,可求得点
,可求得点![]() 到平面
到平面![]() 的距离,从而求得直线
的距离,从而求得直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:如图, ∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵点![]() 、
、![]() 分别在棱
分别在棱![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,,∴
,,∴![]() ,
,
∴![]() 平面
平面![]() ,又∵
,又∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
在矩形![]() 中,
中,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
且![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)设点![]() 到在平面
到在平面![]() 的距离为
的距离为![]() ,则有
,则有![]() ,而由(1)得
,而由(1)得![]() 平面
平面![]() ,∴
,∴![]() ,而
,而![]() ,
,![]() ,
,
由(1)可得![]() 平面
平面![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() 的长,
的长,
∴![]() ,而
,而![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设甲、乙两位同学上学期间,每天7:30之前到校的概率均为![]() .假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(Ⅰ)用![]() 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量
表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设![]() 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件
为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于项数为m(![]() 且
且![]() )的有穷正整数数列
)的有穷正整数数列![]() ,记
,记![]()
![]() ,即
,即![]() 为
为![]() 中的最小值,设由
中的最小值,设由![]() 组成的数列
组成的数列![]() 称为
称为![]() 的“新型数列”.
的“新型数列”.
(1)若数列![]() 为2019,2020,2019,2018,2017,请写出
为2019,2020,2019,2018,2017,请写出![]() 的“新型数列”
的“新型数列”![]() 的所有项;
的所有项;
(2)若数列![]() 满足
满足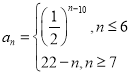 ,且其对应的“新型数列”
,且其对应的“新型数列”![]() 项数
项数![]() ,求
,求![]() 的所有项的和;
的所有项的和;
(3)若数列![]() 的各项互不相等且所有项的和等于所有项的积,求符合条件的
的各项互不相等且所有项的和等于所有项的积,求符合条件的![]() 及其对应的“新型数列”
及其对应的“新型数列”![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 为其前
为其前![]() 项的和,满足
项的和,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:当
,求证:当![]() ,
,![]() 时
时![]() ;
;
(3)已知当![]() ,且
,且![]() 时有
时有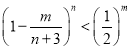 ,其中
,其中![]() ,求满足
,求满足![]() 的所有
的所有![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形![]() 的两个顶点
的两个顶点![]() 、
、![]() 及
及![]() 的中点
的中点![]() 处,
处,![]() ,
,![]() ,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与
,为了处理三家工厂的污水,现要在该矩形区域上(含边界),且与![]() 、
、![]() 等距离的一点
等距离的一点![]() 处,建造一个污水处理厂,并铺设三条排污管道
处,建造一个污水处理厂,并铺设三条排污管道![]() 、
、![]() 、
、![]() .设
.设![]() ∠BAO=x(弧度),排污管道的总长度为
∠BAO=x(弧度),排污管道的总长度为![]() .
.
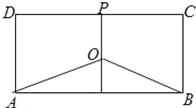
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() 点的位置,使铺设的排污管道的总长度最短,并求总长度的最短公里数(精确到
点的位置,使铺设的排污管道的总长度最短,并求总长度的最短公里数(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,且经过点
的中心在坐标原点,且经过点![]() ,它的一个焦点与抛物线E:
,它的一个焦点与抛物线E:![]() 的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆
的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆![]() 于C、D两点.
于C、D两点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线l经过点![]() ,设点
,设点![]() ,且
,且![]() 的面积为
的面积为![]() ,求k的值;
,求k的值;
(3)若直线l过点![]() ,设直线
,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列,求直线l的方程.
成等差数列,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com