
【题目】如图所示,某海滨城市位于海岸![]() 处,在城市
处,在城市![]() 的南偏西20°方向有一个海面观测站
的南偏西20°方向有一个海面观测站![]() ,现测得与
,现测得与![]() 处相距31海里的
处相距31海里的![]() 处,有一艘豪华游轮正沿北偏西40°方向,以40海里/小时的速度向城市
处,有一艘豪华游轮正沿北偏西40°方向,以40海里/小时的速度向城市![]() 直线航行,30分钟后到达
直线航行,30分钟后到达![]() 处,此时测得
处,此时测得![]() 、
、![]() 间的距离为21海里.
间的距离为21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问这艘游轮再向前航行多少分钟方可到达城市![]() ?
?
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中经X表示。
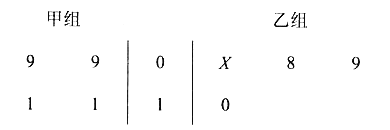
(1)如果X=8,求乙组同学植树棵数的平均数和方差
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在![]() 内,现将成绩按区间
内,现将成绩按区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下的频率分布直方图.
进行分组,绘制成如下的频率分布直方图.

青年组

中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数;
(2)从青年组![]() ,
,![]() 的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自
的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题,其中正确命题的个数是______个.
①线段![]() 在平面
在平面![]() 内,则直线
内,则直线![]() 不在平面
不在平面![]() 内;②两平面有一个公共点,则一定有无数个公共点;③三条平行直线共面;④空间三点确定一个平面.
内;②两平面有一个公共点,则一定有无数个公共点;③三条平行直线共面;④空间三点确定一个平面.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象相邻两条对称轴的距离为
图象相邻两条对称轴的距离为![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后,得到的图象关于y轴对称则函数
个单位后,得到的图象关于y轴对称则函数![]() 的图象( )
的图象( )
A. 关于直线![]() 对称 B. 关于直线
对称 B. 关于直线![]() 对称
对称
C. 关于点![]() 对称 D. 关于点
对称 D. 关于点![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,并且内切于定圆
,并且内切于定圆![]() ..
..
(1)求动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 上存在两个点
上存在两个点![]() ,(1)中曲线上有两个点
,(1)中曲线上有两个点![]() ,并且
,并且![]() 三点共线,
三点共线,![]() 三点共线,
三点共线,![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com