
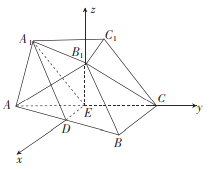
【题目】如图,在三棱台![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点, ![]() 平面
平面![]() ,
, ![]() 是等边三角形,
是等边三角形, ![]() ,
, ![]() ,
,![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)根据棱台的性质和三角形的中位线可以得到![]() ,从而得到
,从而得到![]() 平面
平面![]() .在梯形
.在梯形![]() 中,
中, ![]() (
(![]() 为棱
为棱![]() 的中点),所以
的中点),所以![]() 平面
平面![]() ,从而可以证明平面
,从而可以证明平面![]() 平面
平面![]() ,也就能得到
,也就能得到![]() 平面
平面![]() .(2)以
.(2)以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,通过计算平面
,通过计算平面![]() 和平面
和平面![]() 的法向量的夹角得到二面角
的法向量的夹角得到二面角![]() 的正弦值为
的正弦值为![]() .
.
解析:(1)证明:因为![]() ,
, ![]() 为棱
为棱![]() 的中点,所以
的中点,所以![]() ,所以四边形
,所以四边形![]() 为平行四边形,从而
为平行四边形,从而![]() .又
.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() . 因为
. 因为![]() 是
是![]() 的中位线,所以
的中位线,所以![]() ,同理可证,
,同理可证, ![]() 平面
平面![]() .因为
.因为![]() ,所以平面
,所以平面![]() 平面
平面![]() . 又
. 又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,设
,设![]() ,则
,则![]() ,则
,则![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,则
,则![]() 即
即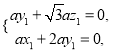
取![]() ,得
,得![]() .
.
同理,设平面![]() 的一个法向量
的一个法向量![]() ,又
,又![]() ,
,
由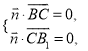 ,得
,得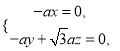 取
取![]() ,得
,得![]() .所以
.所以![]() ,即二面角
,即二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙两名同学准备参加考试,在正式考试之前进行了十次模拟测试,测试成绩如下:
甲:137,121,131,120,129,119,132,123,125,133
乙:110,130,147,127,146,114,126,110,144,146
(1)画出甲、乙两人成绩的茎叶图,求出甲同学成绩的平均数和方差,并根据茎叶图,写出甲、乙两位同学平均成绩以及两位同学成绩的中位数的大小关系的结论;
(2)规定成绩超过127为“良好”,现在老师分别从甲、乙两人成绩中各随机选出一个,求选出成绩“良好”的个数![]() 的分布列和数学期望.
的分布列和数学期望.
(注:方差![]() ,其中
,其中![]() 为
为![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(Ⅰ)求获得复赛资格的人数;
(Ⅱ)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取
的参赛者中,利用分层抽样的方法随机抽取![]() 人参加学校座谈交流,那么从得分在区间
人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(Ⅲ)从(Ⅱ)抽取的![]() 人中,选出
人中,选出![]() 人参加全市座谈交流,设
人参加全市座谈交流,设![]() 表示得分在区间
表示得分在区间![]() 中参加全市座谈交流的人数,求
中参加全市座谈交流的人数,求![]() 的分布列及数学期望E(X).
的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数![]() 满足
满足![]() ,且在[0,1)上单调递减,若方程
,且在[0,1)上单调递减,若方程![]() 在[0,1)上有实数根,则方程
在[0,1)上有实数根,则方程![]() 在区间[-1,7]上所有实根之和是
在区间[-1,7]上所有实根之和是
A. 12 B. 14 C. 6 D. 7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
: ![]()
![]() 的焦距与椭圆
的焦距与椭圆![]() :
: ![]() 的短轴长相等,且
的短轴长相等,且![]() 与
与![]() 的长轴长相等,这两个椭圆在第一象限的交点为
的长轴长相等,这两个椭圆在第一象限的交点为![]() ,直线
,直线![]() 经过
经过![]() 在
在![]() 轴正半轴上的顶点
轴正半轴上的顶点![]() 且与直线
且与直线![]() (
(![]() 为坐标原点)垂直,
为坐标原点)垂直, ![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,
, ![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求![]() 的标准方程;
的标准方程;
(2)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为15.
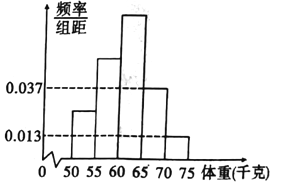
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设![]() 表示体重超过65公斤的学生人数,求
表示体重超过65公斤的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吸烟有害健康,远离烟草,珍惜生命。据统计一小时内吸烟5支诱发脑血管病的概率为0.02,一小时内吸烟10支诱发脑血管病的概率为0.16.已知某公司职员在某一小时内吸烟5支未诱发脑血管病,则他在这一小时内还能继吸烟5支不诱发脑血管病的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com