
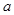 ,BC=2,PA⊥平面ABCD,PA=2,现有数据: ①
,BC=2,PA⊥平面ABCD,PA=2,现有数据: ①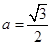 ;②
;②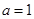 ;③
;③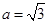 ;建立适当的空间直角坐标系,
;建立适当的空间直角坐标系,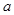 可能取所给数据中的哪些值?请说明理由;
可能取所给数据中的哪些值?请说明理由;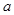 取所给数据的最小值
取所给数据的最小值 时,这样的点Q有几个? 若沿BC方向依次记为
时,这样的点Q有几个? 若沿BC方向依次记为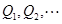 ,试求二面角
,试求二面角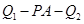 的大小.
的大小.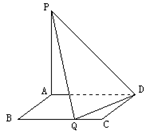
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:不详 题型:解答题
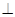 底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点。
底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点。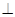 CD;
CD;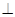 平面PCB,并
平面PCB,并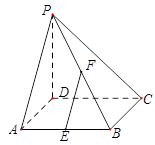
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
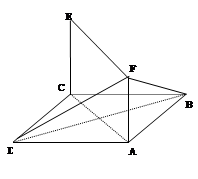
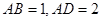 ,
,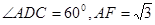 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
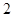 的正方形
的正方形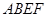 中,
中,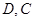 分别为
分别为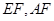 上的点,且
上的点,且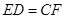 ,现沿
,现沿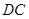 把
把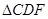 剪切、拼接成如图(2)的图形,再将
剪切、拼接成如图(2)的图形,再将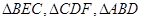 沿
沿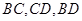 折起,使
折起,使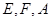 三点重合于点
三点重合于点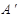 。
。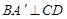 ;
;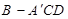 体积的最大值。
体积的最大值。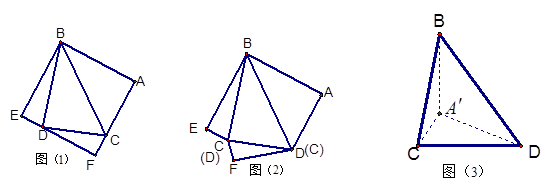
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
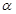 内的两条直线垂直,则
内的两条直线垂直,则 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com