
【题目】某学校为了解高二学生学习效果,从高二第一学期期中考试成绩中随机抽取了25名学生的数学成绩(单位:分),发现这25名学生成绩均在90~150分之间,于是按![]() ,
,![]() ,…,
,…,![]() 分成6组,制成频率分布直方图,如图所示:
分成6组,制成频率分布直方图,如图所示:
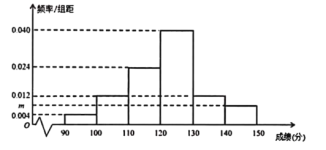
(1)求![]() 的值;
的值;
(2)估计这25名学生数学成绩的平均数;
(3)为进一步了解数学优等生的情况,该学校准备从分数在![]() 内的同学中随机选出2名同学作为代表进行座谈,求这两名同学分数在不同组的概率.
内的同学中随机选出2名同学作为代表进行座谈,求这两名同学分数在不同组的概率.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处的切线
处的切线![]() 与直线
与直线![]() 平行.
平行.
(1)求实数![]() 的值;
的值;
(2)若函数![]() 在
在![]() 上恰有两个零点,求实数
上恰有两个零点,求实数![]() 的取值范围.
的取值范围.
(3)记函数![]() ,设
,设![]() 是函数
是函数![]() 的两个极值点,若
的两个极值点,若![]() ,且
,且![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量.2007年至2018年,某企业连续12年累计研发投入达4100亿元,我们将研发投入与经营收入的比值记为研发投入占营收比.这12年间的研发投入(单位:十亿元)用图中的条形图表示,研发投入占营收比用图中的折线图表示.
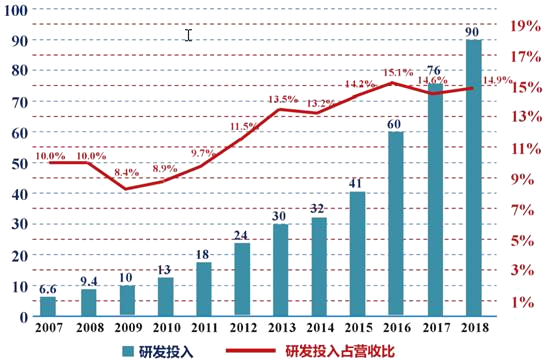
根据折线图和条形图,下列结论错误的是( )
A. 2012﹣2013 年研发投入占营收比增量相比 2017﹣2018 年增量大
B. 该企业连续 12 年研发投入逐年增加
C. 2015﹣2016 年研发投入增值最大
D. 该企业连续 12 年研发投入占营收比逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() 满足
满足![]()
![]()
![]() ,其中
,其中![]() 数列
数列![]() 的前
的前![]() 项和,
项和,
(1)若数列![]() 是首项为
是首项为![]() .公比为
.公比为![]() 的等比数列,求数列
的等比数列,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() 求证:数列
求证:数列![]() 满足
满足![]()
![]()
![]() ,并写出
,并写出![]() 的通项公式;
的通项公式;
(3)在(2)的条件下,设![]() ,求证
,求证![]() 中任意一项总可以表示成该数列其它两项之积.
中任意一项总可以表示成该数列其它两项之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“工资条里显红利,个税新政入民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.某![]() 从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入
从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入![]() (单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
(单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
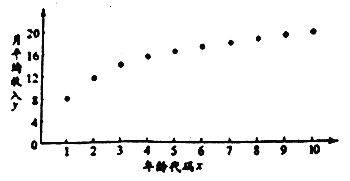
(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据有关数据建立
的关系,试根据有关数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)如果该![]() 从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
附注:①参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,其中
,其中![]() :取
:取![]() ,
,![]() .
.
②参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为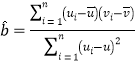 ,
,![]() .
.
③新旧个税政策下每月应纳税所得额(含税)计算方法及税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税 级数 | 每月应纳税所得额(含税) | 税率 | 每月应纳税所得额(含税) | 税率 |
1 | 不超过1500元的都分 | 3 | 不超过3000元的都分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表是某位同学连续5次周考的数学、物理的成绩,结果如下:
周次 | 1 | 2 | 3 | 4 | 5 |
数学( | 79 | 81 | 83 | 85 | 87 |
物理( | 77 | 79 | 79 | 82 | 83 |
参考公式: ,
,![]() ,
,![]() 表示样本均值.
表示样本均值.
(1)求该生5次月考数学成绩的平均分和物理成绩的方差;
(2)一般来说,学生的数学成绩与物理成绩有较强的线性相关关系,根据上表提供的数据,求两个变量![]() 的线性回归方程.
的线性回归方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com