
已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为![]() 和
和![]() ,且满足
,且满足![]() ·
·![]() =t (t≠0且t≠-1). 当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,求t的取值范围.
=t (t≠0且t≠-1). 当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,求t的取值范围.
见解析
当-1<t<0时,曲线C为焦点在x轴上的椭圆,
设![]() =r1,
=r1,![]() = r2, 则r1+ r2=2a=4.
= r2, 则r1+ r2=2a=4.
在△F1PF2中,![]() =2c=4
=2c=4![]() ,
,
∵∠F1PF2=120°,由余弦定理,得4c2=r![]() +r
+r![]() -2r1r2
-2r1r2![]() = r
= r![]() +r
+r![]() + r1r2
+ r1r2
= (r1+r2)2-r1r2≥(r1+r2)2-(![]() )2=3a2, ∴16(1+t)≥12, ∴t≥-
)2=3a2, ∴16(1+t)≥12, ∴t≥-![]() .
.
所以当-![]() ≤t<0时,曲线上存在点Q使∠F1QF2=120°
≤t<0时,曲线上存在点Q使∠F1QF2=120°
当t<-1时,曲线C为焦点在y轴上的椭圆,
设![]() =r1,
=r1,![]() = r2,则r1+r2=2a=-4 t,
= r2,则r1+r2=2a=-4 t,
在△F1PF2中, ![]() =2c=4
=2c=4![]() .
.
∵∠F1PF2=120O,由余弦定理,得4c2=r![]() +r
+r![]() -2r1r2
-2r1r2![]() = r
= r![]() +r
+r![]() + r1r2
+ r1r2
= (r1+r2)2-r1r2≥(r1+r2)2-(![]() )2=3a2, ∴16(-1-t)≥-12t
)2=3a2, ∴16(-1-t)≥-12t![]() t≤-4.
t≤-4.
所以当t≤-4时,曲线上存在点Q使∠F1QF2=120O
综上知当t<0时,曲线上存在点Q使∠AQB=120O的t的取值范围是
![]() .
.


科目:高中数学 来源:2010年辽宁省高二上学期10月月考文科数学卷 题型:解答题
已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为 和
和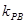 ,且满足
,且满足 ·
·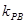 =t (t≠0且t≠-1).
=t (t≠0且t≠-1).
(1)求动点P的轨迹C的方程;
(2)当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,
求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com