
【题目】设![]() 是一些互不相同的四元数组
是一些互不相同的四元数组![]() 的集合,其中,
的集合,其中,![]() 或
或![]() .已知
.已知![]() 的元素个数不超过15,且满足:若
的元素个数不超过15,且满足:若![]() 、
、![]() ,则
,则![]() 、
、![]() ,其中,
,其中,![]() ,
,![]() .求集合
.求集合![]() 元素个数的最大值.
元素个数的最大值.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程为![]() 的曲线,给出下列四个结论:
的曲线,给出下列四个结论:
① 关于![]() 轴对称;
轴对称;
② 关于坐标原点对称;
③ 关于![]() 轴对称;
轴对称;
④ ![]() ,
,![]() ;
;
以上结论正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
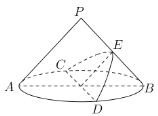
【题目】我们知道:用平行于圆锥母线的平面(不过顶点)截圆锥,则平面与圆锥侧面的交线是抛物线一部分,如图,在底面半径和高均为2的圆锥中,![]()
![]() 是底面圆
是底面圆![]() 的两条互相垂直的直径,
的两条互相垂直的直径,![]() 是母线
是母线![]() 的中点,已知过
的中点,已知过![]() 与
与![]() 的平面与圆锥侧面的交线是以
的平面与圆锥侧面的交线是以![]() 为顶点的圆锥曲线的一部分,则该圆锥曲线的焦点到其准线的距离等于__________.
为顶点的圆锥曲线的一部分,则该圆锥曲线的焦点到其准线的距离等于__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其公共定义域上的任意实数
对其公共定义域上的任意实数![]() 都满足:
都满足:![]() 和
和![]() 恒成立,则称此直线
恒成立,则称此直线![]() 为
为![]() 和
和![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() ,
,![]() ,
,![]() ,下列命题为真命题的是( )
,下列命题为真命题的是( )
A.![]() 在
在![]() 内单调递减
内单调递减
B.![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的最小值为
的最小值为![]()
C.![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的取值范围是
的取值范围是![]()
D.![]() 和
和![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com