
【题目】(本题满分10分)已知半径为![]() 的圆的圆心M在
的圆的圆心M在![]() 轴上,圆心M的横坐标是整数,且圆M与直线
轴上,圆心M的横坐标是整数,且圆M与直线![]() 相切.
相切.
求:(Ⅰ)求圆M的方程;
(Ⅱ)设直线![]() 与圆M相交于
与圆M相交于![]() 两点,求实数
两点,求实数![]() 的取值范围.
的取值范围.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)若f(1)=2,求函数y=f(x)-2x在[![]() ,2]上的值域;
,2]上的值域;
(Ⅱ)当a∈(0,![]() )时,试判断f(x)在(0,1]上的单调性,并用定义证明你的结论.
)时,试判断f(x)在(0,1]上的单调性,并用定义证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】借助计算机(器)作某些分段函数图象时,分段函数的表示有时可以利用函数![]() ,例如要表示分段函数g(x)=
,例如要表示分段函数g(x)=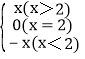 总可以将g(x)表示为g(x)=xh(x-2)+(-x)h(2-x).
总可以将g(x)表示为g(x)=xh(x-2)+(-x)h(2-x).
(1)设f(x)=(x2-2x+3)h(x-1)+(1-x2)h(1-x),请把函数f(x)写成分段函数的形式;
(2)已知G(x)=[(3a-1)x+4a]h(1-x)+logaxh(x-1)是R上的减函数,求a的取值范围;
(3)设F(x)=(x2+x-a+1)h(x-a)+(x2-x+a+1)h(a-x),求函数F(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (k∈R)
(k∈R)
(Ⅰ)若该函数是偶函数,求实数k及f(log32)的值;
(Ⅱ)若函数g(x)=x+log3f(x)有零点,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列4个判断:
①若f(x)=x2-2ax在[1,+∞)上增函数,则a=1;
②函数f(x)=2x-x2只有两个零点;③函数y=2|x|的最小值是1;
④在同一坐标系中函数y=2x与y=2-x的图象关于y轴对称.
其中正确命题的序号是( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com