
分析 (1)由条件去掉绝对值,求得x的范围.
(2)由题意可得|2x-a|+|2x+1|-x-2≥0 恒成立,令h(x)=|2x-a|+|2x+1|-x-2,化简h(x)的解析式,根据单调性求得h(x)的最小值,再令最小值大于或等于零,求得a的范围.
解答 解:(1)|2x-1|≥1,解得 x≤0或x≥1,∴原不等式的解集为{x|x≤0或x≥1}.
(2)由题意可得|2x-a|≥x+2-|2x+1|恒成立,
即|2x-a|+|2x+1|≥x+2恒成立,即|2x-a|+|2x+1|-x-2≥0 恒成立.
令h(x)=|2x-a|+|2x+1|-x-2=$\left\{\begin{array}{l}{-5x+a-3,x≤-\frac{1}{2}}\\{-x+a-1,-\frac{1}{2}<x<\frac{a}{2}}\\{3x-a-1,x≥\frac{a}{2}}\end{array}\right.$,
因为a>0,故当x=$\frac{a}{2}$时,h(x)取得最小值为$\frac{a}{2}$-1,令$\frac{a}{2}$-1≥0,求得a≥2.
点评 本题主要考查绝对值不等式的解法,函数的恒成立问题,根据函数的单调性求函数的最小值,体现了等价转化的数学思想,属于中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
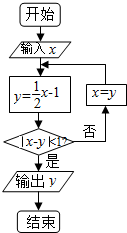 执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )
执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )| A. | 1 | B. | $-\frac{1}{2}$ | C. | $-\frac{5}{4}$ | D. | $-\frac{13}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com