【题目】已知Sn是正项数列{an}的前n项和，且Sn= 
an2+ 
an﹣ 
（1）求数列{an}的通项公式；
（2）若an=2nbn ， 求数列{bn}的前n项和．
【答案】
（1）解：∵Sn= 
+ 
an﹣ 
，
∴Sn﹣1= 
+ an﹣1﹣ ，
∴an=Sn﹣Sn﹣1= （ ﹣ ）+ （an﹣an﹣1）（n≥2），
∵正项数列{an}，
∴an﹣an﹣1=2，易得a1=3，
∴an=2n+1
（2）解：∵an=2nbn
∴bn= 
= 
∴Tn= 
+ 
+…+
Tn= 
+ +…+ 
+
上面两式相减得，
Tn= 
+ 
+ 
+…+ 
﹣ 
= +2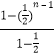 
﹣ ，
∴Tn=5﹣（2n+5） 
【解析】（1）运用an= 
即可求出an；（2）运用数列的求和方法：错位相减法，即可求出数列{bn}的前n项和．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系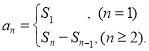
)．
探究与巩固河南科学技术出版社系列答案科目：高中数学 来源： 题型：
【题目】新生儿Apgar评分，即阿氏评分是对新生儿出生后总体状况的一个评估，主要从呼吸、心率、反射、肤色、肌张力这几个方面评分，满10分者为正常新生儿，评分7分以下的新生儿考虑患有轻度窒息，评分在4分以下考虑患有重度窒息，大部分新生儿的评分多在7-10分之间，某市级医院妇产科对1月份出生的新生儿随机抽取了16名，以下表格记录了他们的评分情况.
（1）现从16名新生儿中随机抽取3名，求至多有1名评分不低于9分的概率；
（2）以这16名新生儿数据来估计本年度的总体数据，若从本市本年度新生儿任选3名，记
表示抽到评分不低于9分的新生儿数，求
的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若数列{an}是等差数列，首项a1＞0，a2003+a2004＞0，a2003 ． a2004＜0，则使前n项和Sn＞0成立的最大自然数n是（ ）
A.4005
B.4006
C.4007
D.4008
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两人想参加《中国诗词大会》比赛，筹办方要从10首诗司中分别抽出3首让甲、乙背诵，规定至少背出其中2首才算合格； 在这10首诗词中，甲只能背出其中的7首，乙只能背出其中的8首
（1）求抽到甲能背诵的诗词的数量
的分布列及数学期望；
（2）求甲、乙两人中至少且有一人能合格的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】 用总长14.8米的钢条制作一个长方体容器的框架，如果所制容器底面一边的长比另一边的长多0.5米，那么高为多少时容器的容积最大？最大容积是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设{an}是等差数列，{bn}是各项都为正数的等比数列，且a1=b1=1，a3+b5=21，a5+b3=13．
（1）求{an}、{bn}的通项公式；
（2）求数列 
的前n项和Sn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”．部分统计数据如下表:
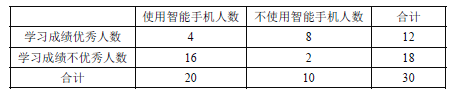
参考数据:
参考公式: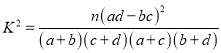 
，其中
(Ⅰ)试根据以上数据，运用独立性检验思想，指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为
组，不使用智能手机且成绩优秀的8位同学记为
组，计划从
组推选的2人和
组推选的3人中，随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验．求挑选的两人恰好分别来自
、
两组的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两家商场对同一种商品开展促销活动，对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘，当指针指向阴影部分(图中两个阴影部分均为扇形，且每个扇形圆心角均为
，边界忽略不计)即为中奖·
乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同)，它是红球的概率是
，若从盒子中一次性摸出2球，且摸到的是2个相同颜色的球，即为中奖.
（Ⅰ）求实数
的值；
（Ⅱ）试问：购买该商品的顾客在哪家商场中奖的可能性大？请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
