
分析 (1)由f(x)=g(x)得$a=\frac{x^2}{{-{e^x}}}$,令$h(x)=\frac{x^2}{{-{e^x}}}(1≤x≤3)$,根据函数的单调性求出a的范围即可;
(2)求出$a=\frac{{{x_1}-{x_2}}}{{{e^{x_1}}-{e^{x_2}}}}$,得到${x_1}+{x_2}=a({e^{x_1}}+{e^{x_2}})=\frac{{{e^{x_1}}+{e^{x_2}}}}{{{e^{x_1}}-{e^{x_2}}}}({x_1}+{x_2})$,令x1-x2=t>0,则${x_1}+{x_2}=\frac{{{e^{x_1}}+{e^{x_2}}}}{{{e^{x_1}}-{e^{x_2}}}}({x_1}-{x_2})=\frac{{({e^t}+1)t}}{{{e^t}-1}}$,问题等价于et(t-2)+t+2>0,根据函数的单调性证明即可.
解答 解:(1)、由f(x)=g(x)得$a=\frac{x^2}{{-{e^x}}}$…(1分)
令$h(x)=\frac{x^2}{{-{e^x}}}(1≤x≤3)$,则$h'(x)=-\frac{{2x{e^x}-{e^x}{x^2}}}{{{e^{2x}}}}=\frac{{{x^2}-2x}}{e^x}=\frac{x(x-2)}{e^x}$…(3分)
当1<x<2时,h'(x)<0;当2<x<3时,h'(x)>0,
所以h(x)在(1,2)递减,(2,3)递增,…(4分)
$h(2)=-\frac{4}{e^2}$$,h(1)=-\frac{1}{e}$,$h(3)=-\frac{9}{e^3}$,因$h(3)-h(1)=\frac{1}{e}-\frac{9}{e^3}=\frac{{{e^2}-9}}{e^3}>0$,…(5分)
所以h(3)>h(1),故方程f(x)=g(x)在[1,3]上有两个否同的实根
等价于$-\frac{4}{e^2}<a<-\frac{1}{e}$,即实数a的取值范围是$(-\frac{4}{e^2},-\frac{1}{e})$…(6分)
(2)、因f(x)有两个不同零点x1,x2,不妨设x1>x2,
所以$\left\{{\begin{array}{l}f({x_1})={x_1}-a{e^{x_1}}=0\\ f({x_2})={x_2}-a{e^{x_2}}=0\end{array}}\right.$,所以$a=\frac{{{x_1}-{x_2}}}{{{e^{x_1}}-{e^{x_2}}}}$…(7分)
${x_1}+{x_2}=a({e^{x_1}}+{e^{x_2}})=\frac{{{e^{x_1}}+{e^{x_2}}}}{{{e^{x_1}}-{e^{x_2}}}}({x_1}+{x_2})$…(8分)
令x1-x2=t>0,则${x_1}+{x_2}=\frac{{{e^{x_1}}+{e^{x_2}}}}{{{e^{x_1}}-{e^{x_2}}}}({x_1}-{x_2})=\frac{{({e^t}+1)t}}{{{e^t}-1}}$…(9分)
则${x_1}+{x_2}=\frac{{({e^t}+1)t}}{{{e^t}-1}}>2$?et(t-2)+t+2>0…(10分)
记h(t)=et(t-2)+t+2,
则h'(t)=et(t-1)+1,h''(t)=ett>0在(0,+∞)恒成立,
故h'(t)在(0,+∞)单调递增,故h'(t)>h'(0)=0,
所以h(t)在(0,+∞)单调递增h(t)>h(0)=0,
所以et(t-2)+t+2>0即x1+x2>2…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
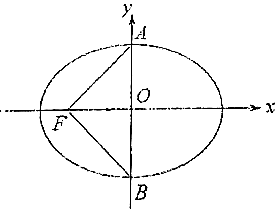 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-2$\sqrt{3}$,0),上下顶点分别为A,B,已知△AFB是等边三角形.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-2$\sqrt{3}$,0),上下顶点分别为A,B,已知△AFB是等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ξ | 10 | 20 | 30 |
| P | 0.6 | a | $\frac{1}{4}$-$\frac{a}{2}$ |
| A. | 42 | B. | 135 | C. | 402 | D. | 405 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,10) | B. | (5,6) | C. | (10,11) | D. | (20,22) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
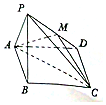 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
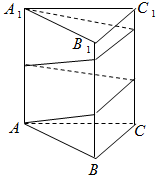 已知正三棱柱ABC-A1B1C1的底面边长为4cm,高为10cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )
已知正三棱柱ABC-A1B1C1的底面边长为4cm,高为10cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )| A. | 16cm | B. | 12$\sqrt{3}$cm | C. | 24$\sqrt{3}$cm | D. | 26cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com