[题目]甲.乙两队进行一场排球比赛.根据以往经验.单局比赛甲队胜乙队的概率为.本场比赛采用五局三胜制.即先胜三局的队获胜.比赛结束.设各局比赛相互间没有影响且无平局.求:(1)前三局比赛甲队领先的概率,(2)设本场比赛的局数为.求的概率分布和数学期望. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】甲、乙两队进行一场排球比赛，根据以往经验，单局比赛甲队胜乙队的概率为.本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束.设各局比赛相互间没有影响且无平局.求：

（1）前三局比赛甲队领先的概率；

（2）设本场比赛的局数为，求的概率分布和数学期望. (用分数表示)

【答案】（1）；（2）详见解析.

【解析】

（1）分为甲队胜三局和甲队胜二局两种情况，概率相加得到答案.

（2）本场比赛的局数为有3,4,5三种情况，分别计算概率得到分布列，最后计算得到答案.

解：（1）设“甲队胜三局”为事件，“甲队胜二局”为事件，

则，，

所以，前三局比赛甲队领先的概率为

（2）甲队胜三局或乙胜三局，

甲队或乙队前三局胜局，第局获胜

甲队或乙队前四局胜局，第局获胜

的分部列为：

数学期望为

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知正项数列的前项和为，若,.

（1）证明：当时，；

（2）求数列的通项公式；

（3）设，求数列的前项和.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了解贵州省某州2020届高三理科生的化学成绩的情况，该州教育局组织高三理科生进行了摸底考试，现从参加考试的学生中随机抽取了100名理科生，，将他们的化学成绩（满分为100分）分为6组，得到如图所示的频率分布直方图.

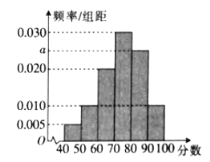
（1）求a的值；

（2）记A表示事件“从参加考试的所有理科生中随机抽取一名学生，该学生的化学成绩不低于70分”，试估计事件A发生的概率；

（3）在抽取的100名理科生中，采用分层抽样的方法从成绩在内的学生中抽取10名，再从这10名学生中随机抽取4名，记这4名理科生成绩在内的人数为X，求X的分布列与数学期望.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间（单位：min）绘制了如下茎叶图：

（1）根据茎叶图判断哪种生产方式的效率更高？并说明理由；

（2）求40名工人完成生产任务所需时间的中位数，并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表：

	超过	不超过
第一种生产方式
第二种生产方式

（3）根据（2）中的列联表，能否有99%的把握认为两种生产方式的效率有差异？

附：，

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是（≈0.618，称为黄金分割比例)，著名的“断臂维纳斯”便是如此．此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是．若某人满足上述两个黄金分割比例，且腿长为105cm，头顶至脖子下端的长度为26 cm，则其身高可能是