
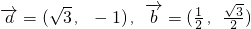 .
. ;
;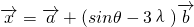 ,
,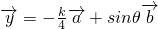 ,且
,且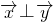 ,试求函数关系式k=f(θ);
,试求函数关系式k=f(θ);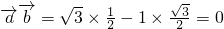

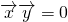
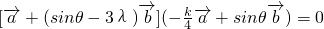
 ,整理可得,
,整理可得,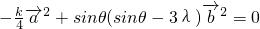

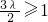 即
即 时,kmin=f(1)=1-3λ
时,kmin=f(1)=1-3λ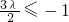 ,即
,即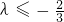 时,kmin=f(-1)=1+3λ
时,kmin=f(-1)=1+3λ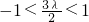 即
即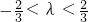 时,
时,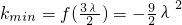 ×
× =
=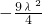
 ,只有证明
,只有证明 即可
即可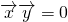 可得
可得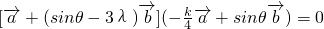 结合(I)
结合(I) 整理可求
整理可求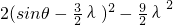 结合-1≤sinθ≤1分①
结合-1≤sinθ≤1分①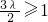 ;②
;②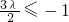 ,③
,③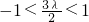 三种情况,结合二次函数的性质进行求解函数的最小值即可
三种情况,结合二次函数的性质进行求解函数的最小值即可

科目:高中数学 来源: 题型:
| m |
| n |
| 3 |
| m |
| n |
| tanx-tan3x |
| 1+2tan2x+tan4x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| d |
| a |
| b |
| c |
| a |
| b |
| d |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OC |
| π |
| 2 |
| ||
| 10 |
| π |
| 4 |
| π |
| 2 |
| OA |
| OC |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年北京市大兴区高一(上)期末数学试卷(必修1、必修4)(解析版) 题型:解答题
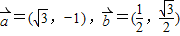 .
. ;
;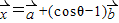 ,
,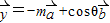 (m≠0,θ∈R)且
(m≠0,θ∈R)且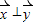 .求出实数m=f(θ)的关系,并求出m的取值范围.
.求出实数m=f(θ)的关系,并求出m的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com