
| A. | “π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期” | |
| B. | “x2+y2=0”是“xy=0”的必要不充分条件 | |
| C. | “若a≤b,则2a≤2b-1”的否命题 | |
| D. | “?a∈(0,+∞),函数y=ax在定义域内单调递增”的否定 |
分析 由复合命题的真假判断说明A、D为真命题;利用充分必要条件的判断方法判断B;写出命题的否命题判断C.
解答 解:对于A,“π是函数y=sinx的一个周期”是假命题,“2π是函数y=cosx的一个周期”是真命题,
∴π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期”是真命题;
对于B,由x2+y2=0,得x=y=0,则xy=0,反之,若xy=0,得x=0或y=0,不一定有x2+y2=0,
∴x2+y2=0”是“xy=0”的充分不必要条件,故B是假命题;
对于C,“若a≤b,则2a≤2b-1”的否命题是:“若a>b,则2a>2b-1”是真命题;
对于D,“?a∈(0,+∞),函数y=ax在定义域内单调递增”为假命题(a=1时y=ax=1),∴其否定为真命题.
故选:B.
点评 本题考查命题的真假判断与应用,考查了充分必要条件的判断方法,考查了命题的否定和否命题,是基础题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a≤\frac{1}{5}$ | B. | $a≥\frac{1}{5}$ | C. | $0<a≤\frac{1}{5}$ | D. | $0≤a≤\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
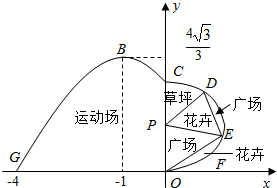 如图,我市体育公园的运动休闲区域的平面图如图所示,在y轴左侧的运动区的边界曲线段是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,$\frac{4\sqrt{3}}{3}$),在y轴右侧的休闲区的边界曲线段是以P为圆心,CO为直径的半圆弧,D、E两点在半圆弧上,满足$\widehat{CE}$=$\widehat{DE}$.
如图,我市体育公园的运动休闲区域的平面图如图所示,在y轴左侧的运动区的边界曲线段是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,$\frac{4\sqrt{3}}{3}$),在y轴右侧的休闲区的边界曲线段是以P为圆心,CO为直径的半圆弧,D、E两点在半圆弧上,满足$\widehat{CE}$=$\widehat{DE}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com