
设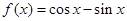 把
把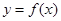 的图象按向量
的图象按向量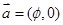 (
(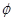 >0)平移后,恰好得到函数
>0)平移后,恰好得到函数 =
=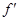 (
( )的图象,则
)的图象,则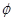 的值可以为( )
的值可以为( )
A.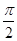 B.
B.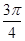 C.π D.
C.π D.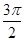
D
【解析】
试题分析:利用三角函数图象变换规律,以及利用函数求导得出 y=-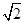 sin(x-φ-
sin(x-φ-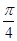 )与f′(x)=-sinx-cosx=-
)与f′(x)=-sinx-cosx=-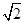 sin(x+
sin(x+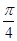 )为同一函数.再利用诱导公式求解.解:f(x)=cosx-sinx=-
)为同一函数.再利用诱导公式求解.解:f(x)=cosx-sinx=-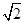 sin(x-
sin(x-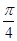 ),f′(x)=-sinx-cosx=-
),f′(x)=-sinx-cosx=-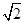 sin(x+
sin(x+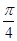 ), 把y=f(x)的图象按向量
), 把y=f(x)的图象按向量 (φ>0)平移,即是把f(x)=cosx-sinx的图象向右平移φ 个单位,得到图象的解析式为y=-
(φ>0)平移,即是把f(x)=cosx-sinx的图象向右平移φ 个单位,得到图象的解析式为y=-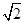 sin(x-φ-
sin(x-φ-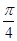 ),由已知,与f′(x)=-sinx-cosx=-
),由已知,与f′(x)=-sinx-cosx=-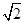 sin(x+
sin(x+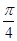 )为同一函数,所以-φ-
)为同一函数,所以-φ-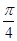 =2kπ+
=2kπ+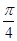 ,取k=-1,可得φ=
,取k=-1,可得φ=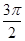
故选D.
考点:三角函数图象变换
点评:本题考查了三角函数图象变换,函数求导,三角函数的图象及性质.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2011-2012学年陕西省高三第十一次大练习理科数学(解析版) 题型:选择题
设 ,把
,把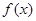 的图象按向量
的图象按向量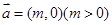 平移后,图象恰好为函数
平移后,图象恰好为函数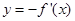 的图象,则
的图象,则 的值可以为 (
) A.
的值可以为 (
) A. B.
B.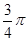 C.
C. D.
D.
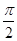
查看答案和解析>>
科目:高中数学 来源:江西省抚州一中2011-2012学年高三第二次月考(数学理) 题型:选择题
设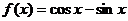 把
把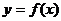 的图象按向量
的图象按向量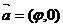 (
(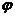 >0)平移后,恰好得到函数
>0)平移后,恰好得到函数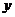 =
=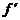 (
(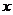 )的图象,则
)的图象,则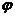 的值可以是(
)
的值可以是(
)
A.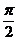 B.
B.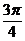 C.π D.
C.π D.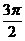
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com