
【题目】已知![]() .
.
(Ⅰ)当![]() 时,判断
时,判断![]() 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)f(x)在(0,+∞)上是单调递增函数
(2)a=-![]() .
.
【解析】
试题分析:(1)利用导数判定函数单调性:先求导数f ′(x)=![]() +
+![]() =
=![]() .因为定义域为(0,+∞),a>0 所以f ′(x)>0,故f(x)在(0,+∞)上是单调递增函数.(2)先分类确定f(x)在[1,e]上的最小值:①若a≥-1,f ′(x)≥0,f(x)在[1,e]上为增函数,f(x)min=f(1)=-a=
.因为定义域为(0,+∞),a>0 所以f ′(x)>0,故f(x)在(0,+∞)上是单调递增函数.(2)先分类确定f(x)在[1,e]上的最小值:①若a≥-1,f ′(x)≥0,f(x)在[1,e]上为增函数,f(x)min=f(1)=-a=![]() ,∴a=-
,∴a=-![]() (舍去).若a≤-e,f ′(x)≤0, f(x)在[1,e]上为减函数,f(x)min=f(e)=1-
(舍去).若a≤-e,f ′(x)≤0, f(x)在[1,e]上为减函数,f(x)min=f(e)=1-![]() =
=![]() ,∴a=-
,∴a=-![]() (舍去).若-e<a<-1,令f ′(x)=0,得x=-a. f(x)min=f(-a)=ln(-a)+1=
(舍去).若-e<a<-1,令f ′(x)=0,得x=-a. f(x)min=f(-a)=ln(-a)+1=![]() a=-
a=-![]() .
.
试题解析:解:(1)由题得f(x)的定义域为(0,+∞),且 f ′(x)=![]() +
+![]() =
=![]() .
.
∵a>0,∴f ′(x)>0,故f(x)在(0,+∞)上是单调递增函数. 3’
(2)由(1)可知:f ′(x)=![]() ,
,
①若a≥-1,则x+a≥0,即f ′(x)≥0在[1,e]上恒成立,此时f(x)在[1,e]上为增函数,
∴f(x)min=f(1)=-a=![]() ,∴a=-
,∴a=-![]() (舍去).
(舍去).
②若a≤-e,则x+a≤0,即f ′(x)≤0在[1,e]上恒成立,此时f(x)在[1,e]上为减函数,
∴f(x)min=f(e)=1-![]() =
=![]() ,∴a=-
,∴a=-![]() (舍去).
(舍去).
③若-e<a<-1,令f′(x)=0,得x=-a.
当1<x<-a时,f ′(x)<0,∴f(x)在(1,-a)上为减函数;
当-a<x<e时,f ′(x)>0,∴f(x)在(-a,e)上为增函数,
∴f(x)min=f(-a)=ln(-a)+1=![]() a=-
a=-![]() .
.
综上可知:a=-![]() . 12’
. 12’


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某商场举行抽奖活动,从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于6中特等奖,等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中二等奖的概率;
(2)求未中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() .
.
(1)若直线![]() 与直线
与直线![]() 平行,求实数
平行,求实数![]() 的值;
的值;
(2)若![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上,已知
上,已知![]() 的中点在
的中点在![]() 轴上,求点
轴上,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据两直线平行,对应方向向量共线,列方程即可求出![]() 的值;(2)根据
的值;(2)根据![]() 时,直线
时,直线![]() 的方程设出点
的方程设出点![]() 的坐标,由此求出
的坐标,由此求出![]() 的中点坐标,再由中点在
的中点坐标,再由中点在![]() 轴上求出点
轴上求出点![]() 的坐标.
的坐标.
试题解析:(1)∵直线![]() 与直线
与直线![]() 平行,
平行,
∴![]() ,
,
∴![]() ,经检验知,满足题意.
,经检验知,满足题意.
(2)由题意可知: ![]() ,
,
设![]() ,则
,则![]() 的中点为
的中点为![]() ,
,
∵![]() 的中点在
的中点在![]() 轴上,∴
轴上,∴![]() ,
,
∴![]() .
.
【题型】解答题
【结束】
16
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
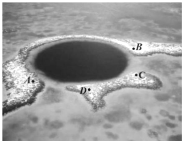
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
| |||||
|
|
| |||
|
(1)请结合所给表格,在所给的坐标系中作出函数![]() 一个周期内的简图;
一个周期内的简图;

(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求![]() 的最大值和最小值及相应
的最大值和最小值及相应![]() 的取值.
的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,前10万元按销售利润的15%进行奖励,若超出部分为t万元,则超出部分按![]() 进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出奖金y关于销售利润x的关系式;
(2)如果业务员小王获得3.5万元的奖金,那么他的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:(x+1)2+(y-3)2=9和圆C2:x2+y2-4x+2y-11=0.
(1)求两圆公共弦所在直线的方程;
(2)求直线过点C(3,-5),且与公共弦垂直的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com