
【题目】现代足球运动是世上开展得最广泛、影响最大的运动项目,有人称它为“世界第一运动”.早在2000多年前的春秋战国时代,就有了一种球类游戏“蹴鞠”,后来经过阿拉伯人传到欧洲,发展成现代足球.1863年10月26日,英国人在伦敦成立了世界上第一个足球运动组织——英国足球协会,并统一了足球规则.人们称这一天是现代足球的诞生日.如图所示,足球表面是由若干黑色正五边形和白色正六边形皮围成的,我们把这些正五边形和正六边形都称为足球的面,任何相邻两个面的公共边叫做足球的棱.已知足球表面中的正六边形的面为20个,则该足球表面中的正五边形的面为______个,该足球表面的棱为______条.

【答案】12 90
【解析】
由题目分析,可设这个足球有正五边形皮子x块,则根据题意可得等量关系式:正六边形的块数×3=正五边形的块数×5,由此可以解出正五边形个数,根据两条边组成一条棱,因此可求棱的条数.
足球每块黑色皮子的5条边分别与5块白色皮子的边缝在一起;
每块白色皮子的6条边中,有3条边与黑色皮子的边缝在一起,
另3条边则与其他白色皮子的边缝在一起.
所以设这个足球有x块正五边形,一共有5x条边,其中白皮三条边和黑皮相连,
又足球表面中的正六边形的面为20个,
根据题意可得方程:![]() ,
,
解得![]() ,
,
该足球表面中的正五边形的面为12个;
因为任何相邻两个面的公共边叫做足球的棱,
所以每条棱由两条边组成,
该足球表面的棱为:![]() 条.
条.
故答案为:12;90.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() ,
,![]() 的中点.
的中点.

(I)证明:直线![]() 与
与![]() 共面;
共面;
(Ⅱ)证明:平面![]() 平面
平面![]() ;并试写出
;并试写出![]() 到平面
到平面![]() 的距离(不必写出计算过程).
的距离(不必写出计算过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心为原点O,焦点在x轴上的椭圆C的离心率为![]() ,且椭圆C的长轴是圆
,且椭圆C的长轴是圆![]() 的一条直径.
的一条直径.
(1)求椭圆C的方程;
(2)若不过原点的直线l与椭圆C交于A,B两点,与圆M交于P、Q两点,且直线OA,AB,OB的斜率成等比数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西湖小学为了丰富学生的课余生活开设课后少年宫活动,其中面向二年级的学生共开设了三门课外活动课:七巧板、健美操、剪纸.203班有包括奔奔、果果在内的5位同学报名参加了少年宫活动,每位同学只能挑选一门课外活动课,已知每门课都有人选,则奔奔和果果选择了同一个课外活动课的选课方法种数为( )
A.18B.36C.72D.144
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已过抛物线![]() :
:![]() 的焦点
的焦点![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,以
两点,以![]() ,
,![]() 两点为切点作抛物线的切线,两条直线交于
两点为切点作抛物线的切线,两条直线交于![]() 点.
点.
(1)当直线![]() 平行于
平行于![]() 轴时,求点
轴时,求点![]() 的坐标;
的坐标;
(2)当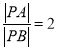 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,
,![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,是否存在定点
两点,是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 斜率之积为定值,若存在,求出
斜率之积为定值,若存在,求出![]() 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ;数列
;数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,问:数列
,问:数列![]() 中是否存在不同两项
中是否存在不同两项![]() ,
,![]() (
(![]() ,i,
,i,![]() ),使
),使![]() 仍是数列
仍是数列![]() 中的项?若存在,请求出i,j;若不存在,请说明理由.
中的项?若存在,请求出i,j;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]()
![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com