
近日,国家经贸委发出了关于深入开展增产节约运动,大力增产市场适销对路产品的通知,并发布了当前国内市场185种适销工业品和42种滞销产品的参考目录。为此,一公司举行某产品的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足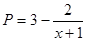 (其中
(其中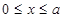 ,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为
,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为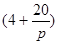 万元/万件.
万元/万件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润是大?
(1)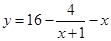 ,(
,(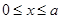 ).
).
(2)当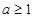 时,促销费用投入1万元时,厂家的利润最大;
时,促销费用投入1万元时,厂家的利润最大;
当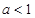 时,促销费用投入
时,促销费用投入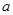 万元时,厂家的利润最大 .
万元时,厂家的利润最大 .
解析试题分析:(1)由题意得到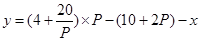 , 将
, 将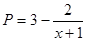 代入化简即得
代入化简即得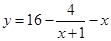 ,(
,(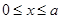 ).
).
(2)将原函数变形,应用基本不等式,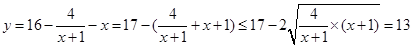 ,
,
当且仅当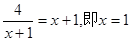 时,上式取等号.根据
时,上式取等号.根据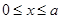 ,讨论
,讨论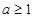 ,
,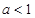 ,的不同情况,确定最大利润.
,的不同情况,确定最大利润.
试题解析:(1)由题意知, 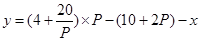 ,
,
将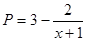 代入化简得:
代入化简得: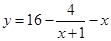 ,(
,(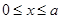 ), 6分
), 6分
(2)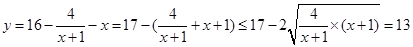 ,
,
当且仅当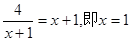 时,上式取等号. 9分
时,上式取等号. 9分
当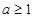 时,促销费用投入1万元时,厂家的利润最大;
时,促销费用投入1万元时,厂家的利润最大;
当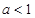 时,
时,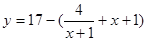 在
在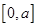 上单调递增,所以在
上单调递增,所以在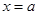 时,函数有最大值.促销费用投入
时,函数有最大值.促销费用投入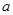 万元时,厂家的利润最大 .
万元时,厂家的利润最大 .
综上述,当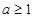 时,促销费用投入1万元时,厂家的利润最大;
时,促销费用投入1万元时,厂家的利润最大;
当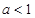 时,促销费用投入
时,促销费用投入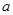 万元时,厂家的利润最大 . 12分
万元时,厂家的利润最大 . 12分
考点:函数的应用问题,基本不等式.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:解答题
(13分)某工厂某种产品的年固定成本为250万元,每生产x千件,需另投入成本C(x),当年产量不足80千件时,C(x)= x2+10x(万元);当年产量不小于80千件时,C(x)=51x+
x2+10x(万元);当年产量不小于80千件时,C(x)=51x+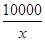 -1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为 米,圆心角为
米,圆心角为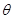 (弧度).
(弧度).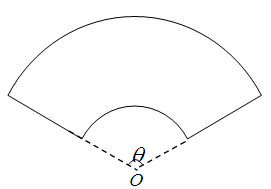
(1)求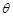 关于
关于 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为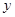 ,求
,求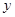 关于
关于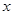 的函数关系式,并求出
的函数关系式,并求出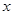 为何值时,
为何值时,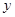 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 是正数,
是正数, ,
, ,
, .
.
(Ⅰ)若 成等差数列,比较
成等差数列,比较 与
与 的大小;
的大小;
(Ⅱ)若 ,则
,则 三个数中,哪个数最大,请说明理由;
三个数中,哪个数最大,请说明理由;
(Ⅲ)若 ,
, ,
, (
( ),且
),且 ,
, ,
, 的整数部分分别是
的整数部分分别是

 求所有
求所有 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com