
【题目】从某高中女学生中选取10名学生,根据其身高![]() 、体重
、体重![]() 数据,得到体重关于身高的回归方程
数据,得到体重关于身高的回归方程![]() ,用来刻画回归效果的相关指数
,用来刻画回归效果的相关指数![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A.这些女学生的体重和身高具有非线性相关关系
B.这些女学生的体重差异有60%是由身高引起的
C.身高为![]() 的女学生的体重一定为
的女学生的体重一定为![]()
D.这些女学生的身高每增加![]() ,其体重约增加
,其体重约增加![]()
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】《周髀算经》中给出了勾股定理的绝妙证明.如图是赵爽弦图及注文.弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成朱色及黄色,其面积称为朱实、黄实.由2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2.若图中勾股形的勾股比为![]() ,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:
,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:![]() ,
,![]() )
)
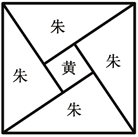
A.2B.4C.6D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,点
中,点![]() 、
、![]() 分别是棱
分别是棱![]() 和
和![]() 的中点,给出下列结论:
的中点,给出下列结论:
①直线![]() 与
与![]() 所成角为
所成角为![]() ;②正方体的所有棱中与直线
;②正方体的所有棱中与直线![]() 异面的有
异面的有![]() 条;③直线
条;③直线![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() .其中正确的是( )
.其中正确的是( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
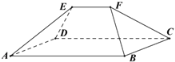
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍[chúméng]”的五面体(如图),四边形![]() 为矩形,棱
为矩形,棱![]() .若此几何体中,
.若此几何体中,![]() ,
,![]() 和
和![]() 都是边长为
都是边长为![]() 的等边三角形,则此几何体的体积为( )
的等边三角形,则此几何体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的零点构成一个公差为
的零点构成一个公差为![]() 的等差数列,把函数
的等差数列,把函数![]() 的图象沿
的图象沿![]() 轴向右平移
轴向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.关于函数
的图象.关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 在![]() 上是增函数B. 其图象关于直线
上是增函数B. 其图象关于直线![]() 对称
对称
C. 函数![]() 是偶函数D. 在区间
是偶函数D. 在区间![]() 上的值域为
上的值域为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)[选修4-5:不等式选讲]
已知函数![]() =|x-a|+
=|x-a|+![]() (a≠0)
(a≠0)
(1)若不等式![]() -
-![]() ≤1恒成立,求实数m的最大值;
≤1恒成立,求实数m的最大值;
(2)当a<![]() 时,函数g(x)=
时,函数g(x)=![]() +|2x-1|有零点,求实数a的取值范围
+|2x-1|有零点,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]()
![]() 为参数,曲线
为参数,曲线![]() 上的点
上的点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)过O作线段![]() 的垂线,垂足为H,求点H的轨迹
的垂线,垂足为H,求点H的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 两点间的距离的取值范围.
两点间的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 且与直线
且与直线![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,点
,点![]()
![]() 为曲线
为曲线![]() 上一点.
上一点.
(1)求![]() 的值及曲线
的值及曲线![]() 的方程;
的方程;
(2)若![]() 为曲线
为曲线![]() 上异于
上异于![]() 的两点,且
的两点,且![]() .记点
.记点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,判断
,判断![]() 是否为定值,若是,请求出该定值;若不是,请说明理由.
是否为定值,若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com