
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
科目:高中数学 来源: 题型:
【题目】给出下列不等式:①x≥ln(x+1)(x>﹣1)② ![]() >﹣
>﹣ ![]() +2x﹣
+2x﹣ ![]() (x>0)③ln
(x>0)③ln ![]() >2(x+
>2(x+ ![]() )(x∈(0,1))其中成立的个数是( )
)(x∈(0,1))其中成立的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的图象过点(0,﹣1).
的图象过点(0,﹣1).
(1)求实数a的值;
(2)若f(x)=m+ ![]() (m,n是常数),求实数m,n的值;
(m,n是常数),求实数m,n的值;
(3)用定义法证明:函数f(x)在(3,+∞)上是单调减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a是常数,且a>0).对于下列命题:①函数f(x)的最小值是﹣1;②函数f(x)在R上是单调函数;③若f(x)>0在[
(a是常数,且a>0).对于下列命题:①函数f(x)的最小值是﹣1;②函数f(x)在R上是单调函数;③若f(x)>0在[ ![]() ,+∞)上恒成立,则a的取值范围是a>1;④对任意x1<0,x2<0且x1≠x2 , 恒有f(
,+∞)上恒成立,则a的取值范围是a>1;④对任意x1<0,x2<0且x1≠x2 , 恒有f( ![]() )>
)> ![]() .其中正确命题的序号是( )
.其中正确命题的序号是( )
A.①②
B.①③
C.③④
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,具有线性相关关系,下表为抽样试验的结果:
转速x(转/秒) | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数y(件) | 5 | 7 | 8 | 9 | 11 |
参考公式: ![]() ,
, ![]() =
= 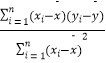 =
= 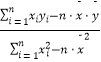 .
.
(1)如果y对x有线性相关关系,求回归方程;
(2)若实际生产中,允许每小时生产的产品中有缺点的零件最多有10个,那么机器的运转速度应控制在设么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)是定义在R上的可导函数,且满足(x﹣1)f′(x)≥0,则必有( )
A.f(0)+f(2)<2f(1)
B.f(0)+f(2)>2f(1)
C.f(0)+f(2)≤2f(1)
D.f(0)+f(2)≥2f(1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=2n2+n,n∈N* , 数列{bn}满足an=4log2bn+3,n∈N* .
(1)求an , bn;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知[x)表示大于x的最小整数,例如[3)=4,[﹣1,3)=﹣1,下列命题中正确的是( ) ①函数f(x)=[x)﹣x的值域是(0,1]
②若{an}是等差数列,则{[an)}也是等差数列
③若{an}是等比数列,则{[an)}也是等比数列
④若x∈(1,2017),则方程[x)﹣x=sin ![]() x有1007个根.
x有1007个根.
A.②
B.③④
C.①
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin( ![]() ﹣x)sinx﹣
﹣x)sinx﹣ ![]() cos2x. (I)求f(x)的最小正周期和最大值;
cos2x. (I)求f(x)的最小正周期和最大值;
(II)讨论f(x)在[ ![]() ,
, ![]() ]上的单调性.
]上的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com