
【题目】设函数f(x)=emx+x2﹣mx.
(1)证明:f(x)在(﹣∞,0)单调递减,在(0,+∞)单调递增;
(2)若对于任意x1 , x2∈[﹣1,1],都有|f(x1)﹣f(x2)|≤e﹣1,求m的取值范围.
【答案】
(1)证明:f′(x)=m(emx﹣1)+2x.
若m≥0,则当x∈(﹣∞,0)时,emx﹣1≤0,f′(x)<0;当x∈(0,+∞)时,emx﹣1≥0,f′(x)>0.
若m<0,则当x∈(﹣∞,0)时,emx﹣1>0,f′(x)<0;当x∈(0,+∞)时,emx﹣1<0,f′(x)>0.
所以,f(x)在(﹣∞,0)时单调递减,在(0,+∞)单调递增
(2)解:由(1)知,对任意的m,f(x)在[﹣1,0]单调递减,在[0,1]单调递增,故f(x)在x=0处取得最小值.
所以对于任意x1,x2∈[﹣1,1],|f(x1)﹣f(x2)|≤e﹣1的充要条件是 ![]()
即 ![]()
设函数g(t)=et﹣t﹣e+1,则g′(t)=et﹣1.
当t<0时,g′(t)<0;当t>0时,g′(t)>0.故g(t)在(﹣∞,0)单调递减,在(0,+∞)单调递增.
又g(1)=0,g(﹣1)=e﹣1+2﹣e<0,故当t∈[﹣1,1]时,g(t)≤0.
当m∈[﹣1,1]时,g(m)≤0,g(﹣m)≤0,即合式成立;
当m>1时,由g(t)的单调性,g(m)>0,即em﹣m>e﹣1.
当m<﹣1时,g(﹣m)>0,即e﹣m+m>e﹣1.
综上,m的取值范围是[﹣1,1]
【解析】(1)利用f′(x)≥0说明函数为增函数,利用f′(x)≤0说明函数为减函数.注意参数m的讨论;(2)由(1)知,对任意的m,f(x)在[﹣1,0]单调递减,在[0,1]单调递增,则恒成立问题转化为最大值和最小值问题.从而求得m的取值范围.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD﹣A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈[0,1],给出以下四个命题:
①平面MENF⊥平面BDD′B′;
②当且仅当x= ![]() 时,四边形MENF的面积最小;
时,四边形MENF的面积最小;
③四边形MENF周长l=f(x),x∈0,1]是单调函数;
④四棱锥C′﹣MENF的体积v=h(x)为常函数;
以上命题中真命题的序号为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx+c在点x=2处取得极值c﹣16.
(1)求a,b的值;
(2)若f(x)有极大值28,求f(x)在[﹣3,3]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() ,曲线
,曲线![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为![]() 轴正半轴建立平面直角坐标系
轴正半轴建立平面直角坐标系![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为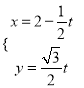 (
(![]() 为参数).
为参数).
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 与
与![]() 交于不同的四点,这四点在
交于不同的四点,这四点在![]() 上排列顺次为
上排列顺次为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代太极图是一种优美的对称图.如果一个函数的图像能够将圆的面积和周长分成两个相等的部分,我们称这样的函数为圆的“太极函数”.下列命题中错误命题的个数是( )
![]() 对于任意一个圆其对应的太极函数不唯一;
对于任意一个圆其对应的太极函数不唯一;
![]() 如果一个函数是两个圆的太极函数,那么这两个圆为同心圆;
如果一个函数是两个圆的太极函数,那么这两个圆为同心圆;
![]() 圆
圆![]() 的一个太极函数为
的一个太极函数为![]() ;
;
![]() 圆的太极函数均是中心对称图形;
圆的太极函数均是中心对称图形;
![]() 奇函数都是太极函数;
奇函数都是太极函数;
![]() 偶函数不可能是太极函数.
偶函数不可能是太极函数.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15. 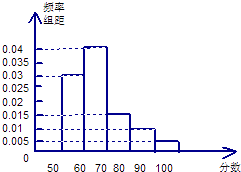
(1)求成绩在50~70分的频率是多少;
(2)求这三个年级参赛学生的总人数是多少;
(3)求成绩在80~100分的学生人数是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com