练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）= 的图象上有且仅有四个不同的点关于直线y=﹣1的对称点在y=kx﹣1的图象上，则实数k的取值范围是（ ）
    A.
    B.
    C.
    D.

    【答案】A
    【解析】解：∵函数f（x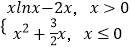）= 的图象上有且仅有四个不同的点关于直线y=﹣1的对称点在y=kx﹣1的图象上，

    而函数y=kx﹣1关于直线y=﹣1的对称图象为y=﹣kx﹣1，

    ∴f（x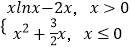）= 的图象与y=﹣kx﹣1的图象有且只有四个不同的交点，

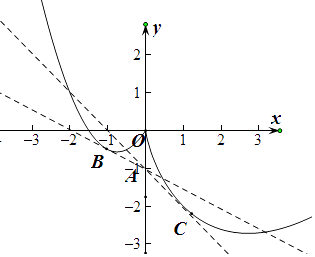
    作函数f（x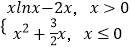）= 的图象与y=﹣kx﹣1的图象如下，

    易知直线y=﹣kx﹣1恒过点A（0，﹣1），

    设直线AC与y=xlnx﹣2x相切于点C（x，xlnx﹣2x），

    y′=lnx﹣1，

    故lnx﹣1= ，

    解得，x=1；

    故kAC=﹣1；

    设直线AB与y=x2+ x相切于点B（x，x2+ x），

    y′=2x+ ，

    故2x+ = ，

    解得，x=﹣1；

    故kAB=﹣2+ =﹣ ；

    故﹣1＜﹣k＜﹣ ，

    故 ＜k＜1；

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（x﹣2）lnx﹣ax+1．
    （1）若f（x）在区间（1，+∞）上单调递增，求实数a的取值范围；
    （2）若存在唯一整数x0 ， 使得f（x0）＜0成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三角形ABC中，角A、B、C的对边分别为a，b，c，a=4bcosC，
    （1）求角B 的值；
    （2）若 ，求三角形ABC 的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=25﹣x ， g（x）=x+t，设h（x）=max{f（x），g（x）}．若当x∈N+时，恒有h（5）≤h（x），则实数t的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的不等式|x+a|＜b的解集为{x|2＜x＜4}．
    （1）求实数a，b的值；
    （2）求证： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆E： + =1（a＞b＞0）上点P，其左、右焦点分别为F1 ， F2 ， △PF1F2的面积的最大值为 ，且满足 =3
    （1）求椭圆E的方程；
    （2）若A，B，C，D是椭圆上互不重合的四个点，AC与BD相交于F1 ， 且 =0，求 的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数 ，记Ik=|fk（a2）﹣fk（a1）|+|fk（a3）﹣fk（a2）|++|fk（a2016）﹣fk（a2015）|，k=1，2，则（ ）
    A.I1＜I2
    B.I1＞I2
    C.I1=I2
    D.I1 ， I2大小关系不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知甲，乙两辆车去同一货场装货物，货场每次只能给一辆车装货物，所以若两辆车同时到达，则需要有一车等待．已知甲、乙两车装货物需要的时间都为30分钟，倘若甲、乙两车都在某1小时内到达该货场，则至少有一辆车需要等待装货物的概率是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=axln（x+1）+x+1（x＞﹣1，a∈R）．
    （1）若 ，求函数f（x）的单调区间；
    （2）当x≥0时，不等式f（x）≤ex恒成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案