【题目】已知实数
满足约束条件：
．
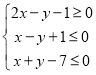（1）请画出可行域，并求
的最小值；
（2）若
取最大值的最优解有无穷多个，求实数
的值.
【答案】（1）可行域见解析，
；（2）
.
【解析】
试题分析：(1)先根据约束条件画出可行域,
,利用
的几何意义求最值,只需求出何时可行域内的点与点
连线的斜率的值最小,从而得到
的最小值；（2）先根据约束条件画出可行域,设
,再利用
的几何意义求最值,只需求出直线与可行域的边界
平行时,最优解有无穷多个,从而得到
值即可.
试题解析：解：（1）如图求画出可行域：．．．．．．．．．．．．．．．．． 2分
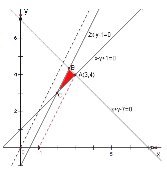
∵表示
与
连线的斜率，如图示，
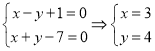，即
，
∴当
时，
．．．．．．．．．．．．．．．．．．．．．．6分
（2）取
得直线
，
∵当取得最值的最优解有无穷多个时，直线
与可行域边界所在直线平行，如图所示，当
，即
时，
取最小值的最优解有无穷多个，不合题意，．．．．．．．．．．．．．． 8分
当
，即
时，
取最大值的最优解有无穷多个，符合题意．．．．．．．．．．．．．．．10分
当
，即
时，
取最大值的最优解有无穷多个，符合题意．
综上得，．．．．．．．．．．．．．．．．．．．．．．．12分
科目：高中数学 来源： 题型：
【题目】设椭圆
的左、右焦点分别为
，右顶点为
，上顶点为
，已知
．
（1）求椭圆的离心率；
（2）设
为椭圆上异于其顶点的一点，以线段
为直径的圆经过点
，经过原点
的直线
与该圆相切，求直线的斜率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
，
．
（1）当
，
时，求函数
的单调区间；
（2）当
时，若
对任意
恒成立，求实数
的取值范围；
（3）设函数
的图象在两点
，
处的切线分别为
，
，若
，
，且
，求实数
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某科研机构研发了某种高新科技产品，现已进入实验阶段.已知实验的启动资金为10万元，从实验的第一天起连续实验，第
天的实验需投入实验费用为
元
，实验30天共投入实验费用17700元.
（1）求
的值及平均每天耗资最少时实验的天数；
（2）现有某知名企业对该项实验进行赞助，实验
天共赞助
元
.为了保证产品质量，至少需进行50天实验，若要求在平均每天实际耗资最小时结束实验，求
的取值范围.（实际耗资=启动资金+试验费用-赞助费）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】学校为了了解高一新生男生得到体能状况，从高一新生中抽取若干名男生进行铅球测试，把所得数据（精确到0.1米）进行整理后，分成6组画出频率分布直方图的一部分（如下图），已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30，第6小组的频数是7.
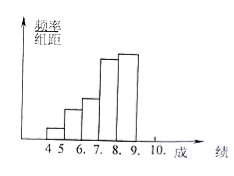
（1）请将频率分布直方图补充完整；
（2）该校参加这次铅球测试的男生有多少人？
（3）若成绩在8.0米以上（含8.0米）的为合格，试求这次铅球测试的成绩的合格率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知动圆过点
，且被
轴截得的线段长为4，记动圆圆心的轨迹为曲线
．
（1）求曲线
的方程；
（2）问： 
轴上是否存在一定点
，使得对于曲线
上的任意两点
和
，当
时，恒有
与
的面积之比等于
？若存在，则求
点的坐标，否则说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
