
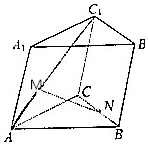
 如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).
如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).分析 ①利用向量的线性运算即可得出,向量$\overrightarrow{MN}$是否与向量$\overrightarrow{AB}$,$\overrightarrow{A{A}_{1}}$共面.
②由①得向量$\overrightarrow{MN}$是否与向量$\overrightarrow{AB}$,$\overrightarrow{A{A}_{1}}$共面.,且MN?面ABB1A1可判定.
解答 解:①$\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=\overrightarrow{AB}+k(\overrightarrow{AC}-\overrightarrow{AB})$=(1-k)$\overrightarrow{AB}$+k$\overrightarrow{AC}$.
$\overrightarrow{AM}=k\overrightarrow{A{C}_{1}}=k(\overrightarrow{A{A}_{1}}+\overrightarrow{AC})$,
∴$\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}=(1-k)\overrightarrow{AB}-k\overrightarrow{A{A}_{1}}$∴向量$\overrightarrow{MN}$是否与向量$\overrightarrow{AB}$,$\overrightarrow{A{A}_{1}}$共面.
②由①得向量$\overrightarrow{MN}$是否与向量$\overrightarrow{AB}$,$\overrightarrow{A{A}_{1}}$共面.,且MN?面ABB1A1
∴直线MN是否与平面ABB1A1平行.
点评 本题考查了空间向量的线性运算,及向量共面的判定、本质意义,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [1,+∞) | C. | (1,5)∪(5,+∞) | D. | [1,5)∪(5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 无数个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{4}$,0) | B. | [-$\frac{3}{4}$,0] | C. | [-$\frac{1}{2}$,1) | D. | [-$\frac{1}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com