
【题目】某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米.已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元.
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米的平均开发费用最低,该写字楼应建为多少层?
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn为数列{an}的前n项和,则![]() 的最小值为( )
的最小值为( )
A.4B.3C.![]() D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax2+(1-a)x+a-3.
(1)若不等式f(x)≥-3对一切实数x恒成立,求实数a的取值范围;
(2)解关于x的不等式f(x)<a-2(a∈R).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为菱形,且∠ABC=60°,
中,底面ABCD为菱形,且∠ABC=60°,![]() 平面ABCD,
平面ABCD,![]() ,点E,F为PC,PA的中点.
,点E,F为PC,PA的中点.
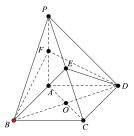
(1)求证:平面BDE⊥平面ABCD;
(2)二面角E—BD—F的大小;
(3)设点M在PB(端点除外)上,试判断CM与平面BDF是否平行,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线
轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)把曲线![]() 的方程化为普通方程,
的方程化为普通方程,![]() 的方程化为直角坐标方程
的方程化为直角坐标方程
(2)若曲线![]() ,
,![]() 相交于
相交于![]() 两点,
两点,![]() 的中点为
的中点为![]() ,过
,过![]() 点作曲线
点作曲线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com