
已知函数![]() ,在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线2x+y=0平行.
,在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线2x+y=0平行.
(Ⅰ)求a的值及切线l的方程;
(Ⅱ)求函数f(x)的极大值和极小值.
|
(Ⅰ)∵切线l与直线 2x+y=0平行, ∴f′(x)=ax2+4x+2=-2,即ax2+4x+4=0. 2分 又这样的切线l仅有一条, ∴△16-16=0,得a=1. 将a=1代入ax2+4x+4=0,得x=-2. 从而y= 故 (Ⅱ)f′(x)=x2+4x+2 由f′(x)>0,得x<-2- ∴函数f(x)在(-∞,-2- -2+ 故f(x)极大=f(-2- f(x)极小=f(-2+ |


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:山东省济宁市汶上一中2012届高三11月月考数学理科试题 题型:044
已知函数![]()
(1)若曲线y=f(x)在点(1,f(1))处的切线的倾斜角为![]() ,求实数a的值;
,求实数a的值;
(2)若函数y=f(x)在区间(0,2]上单调递增,求实数实数a的范围.
查看答案和解析>>
科目:高中数学 来源:陕西省西安铁一中国际合作学校2013届高三上学期期末考试数学(理)试题 题型:044
已知函数![]() .
.
(Ⅰ)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)+x2-2x,若对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷三文科数学 题型:解答题
(本小题满分14分)已知函数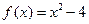 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ÎN *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ÎN *),x1=4.
(Ⅰ)用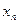 表示xn+1;
表示xn+1;
(Ⅱ)记an=lg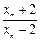 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若bn=xn-2,试比较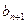 与
与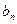 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷三文科数学 题型:解答题
(本小题满分14分)已知函数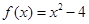 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n Î N *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n Î N *),x1=4.
(Ⅰ)用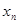 表示xn+1;
表示xn+1;
(Ⅱ)记an=lg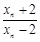 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若bn=xn-2,试比较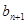 与
与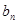 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com