
【题目】已知点P是圆F1:(x﹣1)2+y2=8上任意一点,点F2与点F1关于原点对称,线段PF2的垂直平分线分别与PF1 , PF2交于M,N两点.
(1)求点M的轨迹C的方程;
(2)过点 ![]() 的动直线l与点M的轨迹C交于A,B两点,在y轴上是否存在定点Q,使以AB为直径的圆恒过这个点?若存在,求出点Q的坐标;若不存在,请说明理由.
的动直线l与点M的轨迹C交于A,B两点,在y轴上是否存在定点Q,使以AB为直径的圆恒过这个点?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:由题意得 ![]() ,
,
∴点M的轨迹C为以F1,F2为焦点的椭圆∵ ![]() ,
,
∴点M的轨迹C的方程为 ![]() .
.
(2)直线l的方程可设为 ![]() ,设A(x1,y1),B(x2,y2),
,设A(x1,y1),B(x2,y2),
联立 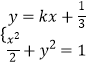 可得9(1+2k2)x2+12kx﹣16=0.
可得9(1+2k2)x2+12kx﹣16=0.
由求根公式化简整理得 ![]() ,
,
假设在y轴上是否存在定点Q(0,m),使以AB为直径的圆恒过这个点,则 ![]() 即
即 ![]() .
.
∵ ![]() ,
,
![]() =
= ![]() =
= ![]() =
= ![]() .
.
∴ ![]() 求得m=﹣1.
求得m=﹣1.
因此,在y轴上存在定点Q(0,﹣1),使以AB为直径的圆恒过这个点.
【解析】(1)根据中垂线的性质不难得到动点到两定点的距离之和为定值,且定值大于这两定点的距离,可得出动点的运动轨迹为椭圆,结合已知可得到轨迹方程,(2)将直线l的方程可设为 y = k x +![]() ,设出A、B两点的坐标,联立直线方程与椭圆方程,使用韦达定理得出A、B横坐标的和与积,假设在y轴上存在定点Q(0,m),则表示出
,设出A、B两点的坐标,联立直线方程与椭圆方程,使用韦达定理得出A、B横坐标的和与积,假设在y轴上存在定点Q(0,m),则表示出![]() ,
,![]() ,且
,且![]() ·
·![]() =0,可解得定点Q的坐标.
=0,可解得定点Q的坐标.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1+2a2+…+nan=(n﹣1)2n+1+2,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn= ![]() ,Tn=b1+b2+…+bn , 求证:对任意的n∈N* , Tn<
,Tn=b1+b2+…+bn , 求证:对任意的n∈N* , Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将y=cosx的图象上的所有点的纵坐标不变,横坐标缩小到原来的一半,然后再将所得图象向左平移 ![]() 个单位长度,则最后所得图象的解析式为( )
个单位长度,则最后所得图象的解析式为( )
A.y=cos(2x+ ![]() )
)
B.y=cos( ![]() +
+ ![]() )
)
C.y=sin2x
D.y=﹣sin2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:
质量指标值m | m<185 | 185≤m<205 | M≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
(1)根据以上抽样调查的数据,能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品的质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如下表: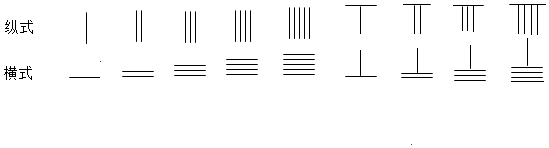
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推,例如6613用算筹表示就是: ![]() ,则算筹式
,则算筹式 ![]() 表示的数字为 .
表示的数字为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣2)ex﹣ ![]() x2 , 其中a∈R,e为自然对数的底数
x2 , 其中a∈R,e为自然对数的底数
(Ⅰ)函数f(x)的图象能否与x轴相切?若能与x轴相切,求实数a的值;否则,请说明理由;
(Ⅱ)若函数y=f(x)+2x在R上单调递增,求实数a能取到的最大整数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 数列{bn}是等比数列,满足a1=3,b1=1,b2+S2=10,a5﹣2b2=a3 .
(1)求数列{an}和{bn}的通项公式;
(2)令cn=anbn , 设数列{cn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数是( )
①命题“x0∈R, ![]() +1>3x0”的否定是“x∈R,x2+1≤3x”;
+1>3x0”的否定是“x∈R,x2+1≤3x”;
②“函数f(x)=cos2ax-sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
③x2+2x≥ax在x∈[1,2]上恒成立(x2+2x)min≥(ax)max在x∈[1,2]上恒成立;
④“平面向量a与b的夹角是钝角”的充要条件是“a·b<0”.
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com