
分析 (1)化方程f(x)=1可化为x2+(x-1)•|x-2|=1,即2x2-3x+2=1(x≥2)或3x-2=1(x<2),从而求解;
(2)f(x)=x2+(x-1)•|x-a|=$\left\{\begin{array}{l}(a+1)x-a,x<a\\ 2{x}^{2}-(a+1)x+a,x≥a\end{array}\right.$,则 $\left\{\begin{array}{l}a+1>0\\ \frac{a+1}{4}≤a\\(a+1)a-a≤2{a}^{2}-(a+1)a+a\end{array}\right.$,从而求a;
解答 解:(1)若a=2,则方程f(x)=1可化为x2+(x-1)•|x-2|=1,
即2x2-3x+2=1(x≥2)或3x-2=1(x<2),
故x=1,或x=$\frac{1}{2}$(舍去);
(2)∵f(x)=x2+(x-1)•|x-a|=$\left\{\begin{array}{l}(a+1)x-a,x<a\\ 2{x}^{2}-(a+1)x+a,x≥a\end{array}\right.$,
则若使函数f(x)在R上单调递增,
则 $\left\{\begin{array}{l}a+1>0\\ \frac{a+1}{4}≤a\\(a+1)a-a≤2{a}^{2}-(a+1)a+a\end{array}\right.$,
则a≥$\frac{1}{3}$;
点评 本题考查了函数导数的综合应用,同时考查了分类讨论的数学思想,属于中档题


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{\sqrt{5}}{5}$) | D. | (0,$\frac{\sqrt{6}}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
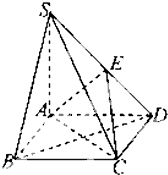 如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.
如图,在底面是菱形的四棱锥S-ABCD中,SA=AB=2,$SB=SD=2\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com