
解:作出一元二次不等式组![]() 所表示的平面区域(如图),即可行域.
所表示的平面区域(如图),即可行域.
考虑z=2x-3y,将它变形为y=![]() x-
x-![]() z,这是斜率为
z,这是斜率为![]() ,随z变化的一组平行直线.-
,随z变化的一组平行直线.-![]() z是直线在y轴上的截距,当直线截距最大时,z的值最小.当然直线要与可行域相交,即在满足约束条件时目标函数z=2x-3y取得最小值;当直线截距最小时,z的值最大.当然直线要与可行域相交,即在满足约束条件时目标函数z=2x-3y取得最大值.
z是直线在y轴上的截距,当直线截距最大时,z的值最小.当然直线要与可行域相交,即在满足约束条件时目标函数z=2x-3y取得最小值;当直线截距最小时,z的值最大.当然直线要与可行域相交,即在满足约束条件时目标函数z=2x-3y取得最大值.
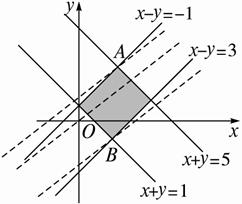
由图可见,当直线z=2x-3y经过可行域上的点A时,截距最大,即z最小.
解方程组![]() 得A的坐标为(2,3).
得A的坐标为(2,3).
所以zmin=2x-3y=2×2-3×3=-5.
当直线z=2x-3y经过可行域上的点B时,截距最小,即z最大.
解方程组![]() 得B的坐标为(2,-1).
得B的坐标为(2,-1).
所以zmax=2x-3y=2×2-3×(-1)=7.


科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省厦门二中高二(上)数学限时训练(8)(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com