
【题目】设等差数列{an}前n项和为Sn , 且满足a2=2,S5=15;等比数列{bn}满足b2=4,b5=32.
(1)求数列{an}、{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
【答案】
(1)解:设等差数列{an}的公差为d,
a2=2,S5=15,可得a1+d=2,5a1+ ![]() d=15,
d=15,
解得a1=d=1,
则an=1+(n﹣1)=n;
设等比数列{bn}的公比为q,
由b2=4,b5=32,可得b1q=4,b1q4=32,
解得b1=q=2,
可得bn=b1qn﹣1=2n;
(2)解:anbn=n2n,
前n项和Tn=12+222++n2n,
2Tn=122+223++n2n+1,
相减可得,﹣Tn=2+22++2n﹣n2n+1
= ![]() ﹣n2n+1,
﹣n2n+1,
化简可得,Tn=(n﹣1)2n+1+2.
【解析】(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,运用等差数列和等比数列的通项公式和求和公式,得到方程组,解方程可得首项和公差、公比,即可得到所求通项公式;(2)求得anbn=n2n,运用数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系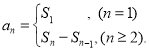 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上. 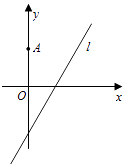
(1)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为π,且其图象向左平移
)的最小正周期为π,且其图象向左平移 ![]() 个单位后得到函数g(x)=cosωx的图象,则函数f(x)的图象( )
个单位后得到函数g(x)=cosωx的图象,则函数f(x)的图象( )
A.关于直线x= ![]() 对称
对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在△ADE区域内参观,在AE上点P处安装一可旋转的监控摄像头,∠MPN为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方,经测量得知:AD=6米,AE=6米,AP=2米,∠MPN= ![]() ,记∠EPM=θ(弧度),监控摄像头的可视区域△PMN的面积为S平方米.
,记∠EPM=θ(弧度),监控摄像头的可视区域△PMN的面积为S平方米. 
(1)求S关于θ的函数关系式,并写出θ的取值范围:(参考数据:tan ![]() ≈3)
≈3)
(2)求S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校统考中,甲、乙两班数学学科前10名的成绩如表:
(I)若已知甲班10位同学数学成绩的中位数为125,乙班10位同学数学成绩的平均分为130,求x,y的值;
(Ⅱ)设定分数在135分之上的学生为数学尖优生,从甲、乙两班的所有数学尖优生中任两人,求两人在同一班的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过点E(1,0)的直线与圆O:x2+y2=4相交于A、B两点,过点C(2,0)且与AB垂直的直线与圆O的另一交点为D. 
(1)当点B坐标为(0,﹣2)时,求直线CD的方程;
(2)求四边形ABCD面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1= ![]() (n∈N*),若bn+1=(n﹣2λ)(
(n∈N*),若bn+1=(n﹣2λ)( ![]() +1)(n∈N*),b1=﹣
+1)(n∈N*),b1=﹣ ![]() λ,且数列{bn}是单调递增数列,则实数λ的取值范围是
λ,且数列{bn}是单调递增数列,则实数λ的取值范围是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com