
 ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围. 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:不详 题型:解答题
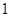 个单位的固体碱在水中逐渐溶化,水中的碱浓度
个单位的固体碱在水中逐渐溶化,水中的碱浓度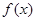 与时间
与时间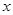 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: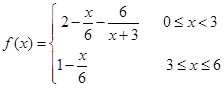 ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于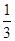 时,才能对污染产生有效的抑制作用.
时,才能对污染产生有效的抑制作用.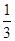 时,马上再投放1个单位的固体碱,设第二次投放后水中碱浓度为
时,马上再投放1个单位的固体碱,设第二次投放后水中碱浓度为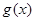 ,求
,求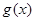 的函数式及水中碱浓度的最大值.(此时水中碱浓度为两次投放的浓度的累加)
的函数式及水中碱浓度的最大值.(此时水中碱浓度为两次投放的浓度的累加)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com