Question

 (I)求函数的单调区间；

  (Ⅱ)函数在区间[1，2]上是否有零点，若有，求出零点，若没有，请说明理由；

  (Ⅲ)若任意的∈(1，2)且≠，证明：(注：

Answer 1

解：.                        

（Ⅰ） .   ……………2分    

，，

在区间和上，；在区间上，

故的单调递增区间是和，单调递减区间是. …………4分

（Ⅱ）先求在的最大值.

由（Ⅰ）可知，

 当时，在上单调递增，在上单调递减，

故.………………6分

由可知，，，

所以，，，                 

故不存在符合条件的，使得.   ………………8分                                 

（Ⅲ）当时，在上单调递增，在上单调递减，

只需证明，都成立，

也可得证命题成立．………………10分        

设，，

在上是减函数，

设，

在上是增函数，

综上述命题成立. ………………12分   

另解:

当时，，

在上单调递减，在上单调递增，

， ，

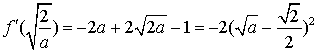
，，.………10分

由导数的几何意义有

对任意，

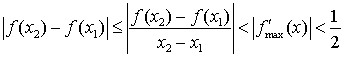．…………12分