
����Ŀ��Ϊ�˽����Ƕ��ڹ����°䲼�ġ����������ſ������ߵ��ȶȣ�����ij�н��е��飬���������50�ˣ��������g��Ƶ���ֲ���֧�֡������������������±�:
���� | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
Ƶ�� | 5 | 10 | 15 | 10 | 5 | 5 |
֧�������������ſ������� | 4 | 5 | 12 | 8 | 2 | 1 |
(1)������ͳ������������2��2�����������ж��Ƿ���99%�İ�����Ϊ��45��Ϊ�ֽ��ԡ����������ſ������ߵ�֧�ֶ��в��죻
���䲻����45������� | �������45������� | �ϼ� | |
֧�� | a= | c= | |
��֧�� | b= | d= | |
�ϼ� |
(2)����������[5,15)�ı������������ѡȡ���˽��е��飬ǡ�������˶�֧�֡����������ſ�"���ߵĸ����Ƕ���?
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
��: ![]() . [��ѧ��113750266]
. [��ѧ��113750266]
���𰸡�(1) û��99%�İ�����Ϊ��45��Ϊ�ֽ��ԡ����������ſ������ߵ�֧�ֶ��в��죻 (2) ![]() .
.
��������
��1�����ù�ʽ���![]() �����ڽ�ֵ�Ƚϣ����ɵõ����ۣ���2�������оٷ���ȷ�������¼��ĸ����������ùŵ�����ʹ�ʽ������������������ѡȡ���˽��е���ʱ��ǡ�������˶�֧���������������ĸ���Ϊ
�����ڽ�ֵ�Ƚϣ����ɵõ����ۣ���2�������оٷ���ȷ�������¼��ĸ����������ùŵ�����ʹ�ʽ������������������ѡȡ���˽��е���ʱ��ǡ�������˶�֧���������������ĸ���Ϊ![]() .
.
(1)2X2����������:
���䲻����45������� | �������45������� | �ϼ� | |
֧�� | a=3 | c=29 | 32 |
��֧�� | b=7 | d=11 | 18 |
�ϼ� | 10 | 40 | 50 |
![]()
����û��99%�İ�����Ϊ��45��Ϊ�ֽ��ԡ����������ſ������ߵ�֧�ֶ��в���.
(2)��������[5��15)��֧�֡����������ſ������ߵ�4�˷ֱ�Ϊa��b��c��d����֧�֡����������ſ������ߵ��˼�ΪM��
���������[5��15)�ı������������ѡȡ�������п��ܵĽ����(a,b)��(a,c)��(a,d)��(a,M)��(b,c)��(b,d) ��(b,M)��(c,d)��(c,M) ��(d,M).
����ǡ�������˶�֧�֡����������ſ�������Ϊ�¼�A�����¼�A���п��ܵĽ����(a,b)��(a,c)��(a,d)��(b,c)��(b,d)��(c,d)������![]() .
.
���Զ�������[15,15)�ı������������ѡȡ���˽��е���ʱ��ǡ�������˶�֧�֡������������ĸ���Ϊ![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʳƷ��Ϊ���˽����¶���������Ӱ�죬�����¼�˸õ�1�·���5�����������![]() ����λ��ǧ�ˣ���õص����������
����λ��ǧ�ˣ���õص����������![]() ����λ��
����λ�� ![]() �������ݣ����±���
�������ݣ����±���
| 2 | 5 | 8 | 9 | 11 |
| 12 | 10 | 8 | 8 | 7 |
��1�����![]() ��
��![]() �Ļع鷽��
�Ļع鷽��![]() ��
��
��2���ж�![]() ��
��![]() ֮��������ػ��Ǹ���أ����õ�1�·�ij����������Ϊ6
֮��������ػ��Ǹ���أ����õ�1�·�ij����������Ϊ6![]() ����������ع鷽��Ԥ��õ굱�յ�Ӫҵ��.
����������ع鷽��Ԥ��õ굱�յ�Ӫҵ��.
��: �ع鷽��![]() ����
����  ,
,![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ҹ�2008����2014������������������������λ���ڶ֣�������ͼ.
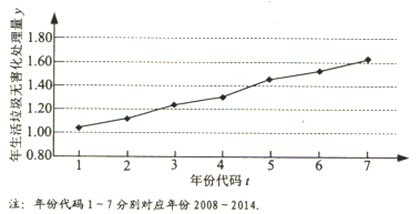
����������ͼ�������������Իع�ģ�����y��t�Ĺ�ϵ���������ϵ������˵����
������y����t�Ļع鷽�̣�ϵ����ȷ��0.01����Ԥ��2016���ҹ�������������������.
��ע��
�ο����ݣ�![]() ��
��![]() ��
��
![]() ��
��![]() ��2.646.
��2.646.
�ο���ʽ�����ϵ��
�ع鷽��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���f��x������f��x+2��=2f��x�����ҵ�x��[2��4]ʱ�� 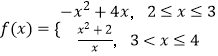 ��g��x��=ax+1����x1��[��2��0]��x2��[��2��1]��ʹ��g��x2��=f��x1������ʵ��a��ȡֵ��ΧΪ�� ��
��g��x��=ax+1����x1��[��2��0]��x2��[��2��1]��ʹ��g��x2��=f��x1������ʵ��a��ȡֵ��ΧΪ�� ��
A.![]()
B.![]()
C.��0��8]
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A.B���ֹ��IJ�Ʒ����Ȣ�ڼס�����̨�����ϸ��ӹ�һ��������ܳ�Ϊ��Ʒ����֪A��Ʒ��Ҫ�ڼ����ϼӹ�3Сʱ�����һ����ϼӹ�1Сʱ��B��Ʒ��Ҫ�ڼ����ϼӹ�1Сʱ�����һ����ϼӹ�3Сʱ����һ���������ڣ���������ֻ��ʹ��11Сʱ���һ�������ֻ��ʹ��9Сʱ��A��Ʒÿ������300Ԫ��B��Ʒÿ������400Ԫ��������̨������һ���������ڴ�������������___________Ԫ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijҽԺij��ʱ����Ӥ��������ʱ�����Ա�Ĺ�ϵ���õ���������ݣ�����ʱ�������ϵ���ӤΪ24�ˣ�ŮӤΪ8�ˣ�����ʱ���ڰ������ӤΪ31�ˣ�ŮӤΪ26�ˣ�
(1)��2��2����������������
�Ա� | ����ʱ�� | �ܼ� | |
���� | ���� | ||
��Ӥ | |||
ŮӤ | |||
�ܼ� | |||
(2)�ܷ��ڷ�����ĸ��ʲ�����0.1��ǰ������ΪӤ���Ա������ʱ���й�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧϰ�澫��ǰ������ij��λ�����Ĺ̶����ξ�������ѧϰ�澫��ʱȫ�ã�
��λ��ѧϰ�澫��ǰ������������ε����������һ������ͳ�ƣ������������£�
������ | ����� | �� �� | |
ѧϰ�澫��ǰ | 50 | 150 | 200 |
ѧϰ�澫���� | 30 | 170 | 200 |
�� �� | 80 | 320 | 400 |
��1����:ѧϰ�澫��ǰ������İٷֱȷֱ��Ƕ���?�������ж��������������ѧϰ�澫���Ƿ��йأ�
��2����˵���Ƿ���97��5%���ϵİ�����Ϊ�������������ѧϰ�澫���йأ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an} Ϊ�ȱ����У��Ȳ�����{bn} ��ǰn ���ΪSn ��n��N* ���������㣺S13=208��S9��S7=41��a1=b2 �� a3=b3 ��
��1��������{an}��{bn} ��ͨ�ʽ��
��2����Tn=a1b1+a2b2+��+anbn ��n��N* ������Tn��
��3����cn= ![]() �����Ƿ����������m��ʹ��cmcm+1cm+2+8=3��cm+cm+1+cm+2����
�����Ƿ����������m��ʹ��cmcm+1cm+2+8=3��cm+cm+1+cm+2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���Sn��pn��q(p��0��p��1)����֤������{an}Ϊ�ȱ����еij�Ҫ����Ϊq����1.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com