
 ,则y与x的函数关系式为
,则y与x的函数关系式为
 +
+ x (
x ( <x<1)
<x<1)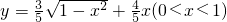
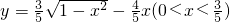
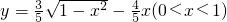
科目:高中数学 来源: 题型:
| 1 |
| TD2 |
| 1 |
| TA2 |
| 1 |
| TB2 |
| 1 |
| TC2 |
| S | 2 △ABC |
| 1 |
| 3 |
| S | 2 △TAB |
| S | 2 △TAC |
| S | 2 △TBC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| 3 |
| 1 |
| 2 |
| m |
| n |
| m |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| π |
| 3 |
| n |
| π |
| 3 |
| m |
| n |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| BC |
| CA |
| CA |
| AB |
| s |
| 3 |
| t |
| C |
| 2 |
| s |
| t |
| 12 |
| 13 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高一版(必修4) 2009-2010学年 第49期 总205期 北师大课标版 题型:044
已知x,y是锐角,且x+y=60°,求S=tanx+tany的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com