
| A. | 0<a2013<$\frac{1}{10}$ | B. | $\frac{1}{10}$≤a2013<1 | C. | 1≤a2013≤10 | D. | a2013>10 |
分析 将数列进行重新分组,根据数列项的规律即可得到结论.
解答 解:将数列进行重新分组,$\frac{1}{1}$,($\frac{2}{1}$,$\frac{1}{2}$),($\frac{3}{1}$,$\frac{2}{2}$,$\frac{1}{3}$),($\frac{4}{1}$,$\frac{3}{2}$,$\frac{2}{3}$,$\frac{1}{4}$),…,以此类推,第N大项$\frac{N}{1}$,$\frac{N-1}{2}$,…,$\frac{1}{N}$,
此时有1+2+3+4+…+N=$\frac{1}{2}$N(N+1),
当N=62时,共有1953项,
当N=63时,共有2016项,
所以数列的第2013项是数列第63组第60个数
故a2013=$\frac{4}{60}$=$\frac{1}{15}$,
故选:A
点评 本题考查数列的递推式,解题时要善于合理地分组,注意总结规律,培养观察总结能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-1,3] | C. | (-1,1) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年入流量X | 40<X<80 | 80≤X≤120 | X>120 |
| 发电机最多 可运行台数 | 1 | 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
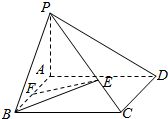 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,且BE⊥PC于E,PA=a,$BE=\frac{{\sqrt{6}}}{3}a$,点F在线段AB上,并有EF∥平面PAD.则$\frac{BF}{FA}$=$\frac{1}{2}$.
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,且BE⊥PC于E,PA=a,$BE=\frac{{\sqrt{6}}}{3}a$,点F在线段AB上,并有EF∥平面PAD.则$\frac{BF}{FA}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com