
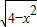 ,x∈[-2,2]与直线y=k(x-2)+4有两个不同的公共点,则实数k的取值范围是 .
,x∈[-2,2]与直线y=k(x-2)+4有两个不同的公共点,则实数k的取值范围是 . 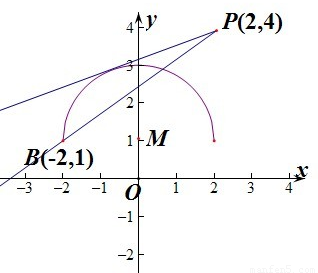 解:因为y=1+
解:因为y=1+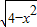 ,所以x2+(y-1)2=4,此时表示为圆心M(0,1),半径r=2的圆.
,所以x2+(y-1)2=4,此时表示为圆心M(0,1),半径r=2的圆.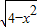 ≥1,所以表示为圆的上部分.
≥1,所以表示为圆的上部分.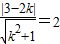 ,解得
,解得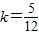 .
.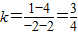 .
.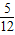 <k≤
<k≤ .
.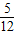 ,
, ].
]. ,
, ].
].

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| BC |
| 1 |
| x |
| A、(2)(4) |
| B、(1)(3)(4) |
| C、(1)(2)(4) |
| D、(2)(3)(4) |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省内江市高一(下)期末数学试卷(理科)(解析版) 题型:填空题
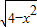 ,x∈[-2,2]与直线y=k(x-2)+4有两个不同的公共点,则实数k的取值范围是 .
,x∈[-2,2]与直线y=k(x-2)+4有两个不同的公共点,则实数k的取值范围是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com