
【题目】若各项均不为零的数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)证明数列![]() 是等比数列,并求
是等比数列,并求![]() 的通项公式;
的通项公式;
(2)设![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对于
对于![]() 恒成立.若存在,求出正整数
恒成立.若存在,求出正整数![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】在中国绿化基金会的支持下,库布齐沙漠得到有效治理.2017年底沙漠的绿化率已达![]() ,从2018年开始,每年将出现这样的情况,上一年底沙漠面积的
,从2018年开始,每年将出现这样的情况,上一年底沙漠面积的![]() 被栽上树改造为绿洲,而同时,上一年底绿洲面积的
被栽上树改造为绿洲,而同时,上一年底绿洲面积的![]() 又被侵蚀,变为沙漠.
又被侵蚀,变为沙漠.
(1)设库布齐沙漠面积为1,由绿洲面积和沙漠面积构成.2017年底绿洲面积为![]() ,经过1年绿洲面积为
,经过1年绿洲面积为![]() ,经过n年绿洲面积为
,经过n年绿洲面积为![]() ,试用
,试用![]() 表示
表示![]() ;
;
(2)问至少需要经过多少年的努力才能使库布齐沙漠的绿洲面积超过![]() (年数取整数).
(年数取整数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大城市往往人口密集,城市绿化在健康人民群众肺方面发挥着非常重要的作用,历史留给我们城市里的大山拥有品种繁多的绿色植物更是无价之宝.改革开放以来,有的地方领导片面追求政绩,对森林资源野蛮开发受到严肃查处事件时有发生.2019年的春节后,广西某市林业管理部门在“绿水青山就是金山银山”理论的不断指引下,积极从外地引进甲、乙两种树苗,并对甲、乙两种树苗各抽测了10株树苗的高度(单位:厘米),数据如下面的茎叶图:
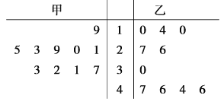
(1)据茎叶图求甲、乙两种树苗的平均高度;
(2)据茎叶图,运用统计学知识分析比较甲、乙两种树苗高度整齐情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京某附属中学为了改善学生的住宿条件,决定在学校附近修建学生宿舍,学校总务办公室用1000万元从政府购得一块廉价土地,该土地可以建造每层1000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高![]() 万元,已知建筑第5层楼房时,每平方米建筑费用为
万元,已知建筑第5层楼房时,每平方米建筑费用为![]() 万元.
万元.
![]() 若学生宿舍建筑为x层楼时,该楼房综合费用为y万元,综合费用是建筑费用与购地费用之和
若学生宿舍建筑为x层楼时,该楼房综合费用为y万元,综合费用是建筑费用与购地费用之和![]() ,写出
,写出![]() 的表达式;
的表达式;
![]() 为了使该楼房每平方米的平均综合费用最低,学校应把楼层建成几层?此时平均综合费用为每平方米多少万元?
为了使该楼房每平方米的平均综合费用最低,学校应把楼层建成几层?此时平均综合费用为每平方米多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com