
分析 (1)化简集合A、B,再根据交集与补集的定义写出对应的结果;
(2)假设存在实数m使得(A∩B)⊆C成立,讨论m=0、m>0和m<0时,
求出集合C,判断是否满足条件即可.
解答 解:(1)因为集合A={x|y=$\frac{1}{\sqrt{-{x}^{2}+x+2}}$}={x|-x2+x+2>0}={x|-1<x<2},
B={y|y=x${\;}^{\frac{1}{3}}$,x∈R}={y|y∈R}=R,
所以A∩B={x|-1<x<2},
所以∁R(A∩B)={x|x≤-1或x≥2};
(2)因为A∩B=(-1,2),
C={x|mx<-1},
假设存在实数m使得(A∩B)⊆C成立,
①当m=0时,C=∅,不符合;
②当m>0时,C={x|<-$\frac{1}{m}$},
于是$\left\{\begin{array}{l}{-\frac{1}{m}≥2}\\{m>0}\end{array}\right.$,无解,不符合;
③当m<0时,C={x|x>-$\frac{1}{m}$},
于是$\left\{\begin{array}{l}{-\frac{1}{m}≤-1}\\{m<0}\end{array}\right.$,无解,不符合;
综上所述,不存在这样的实数m.
点评 本题考查了集合的化简与运算问题,也考查了分类讨论思想的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2-x | B. | y=x-$\frac{1}{x}$ | C. | y=-$\frac{1}{{x}^{2}}$ | D. | y=-tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k<-1 | B. | k≤-1 | C. | k>2 | D. | k≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
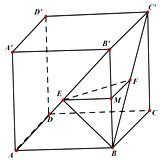 如图,在正方体ABCD-A'B'C'D'中,E,F分别是AB',BC'的中点.
如图,在正方体ABCD-A'B'C'D'中,E,F分别是AB',BC'的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com