
【题目】某水利工程队相应政府号召,计划在韩江边选择一块矩形农田,挖土以加固河堤,为了不影响农民收入,挖土后的农田改造成面积为32400m2的矩形鱼塘,其四周都留有宽3m的路面,问所选的农田的长和宽各为多少时,才能使占有农田的面积最少.
【答案】解:设鱼塘的长为xm,宽为ym,农田面积为s,
则农田长为(x+6)m,宽为(y+6)m,xy=32400,
s=(x+6)(y+6)=xy+6(x+y)+36,
∴ ![]()
![]() ,
,
当且仅当x=y=180时取等号,所以当x=y=180,s=34596m2 ,
答:当选的农田的长和宽都为186m时,才能使占有农田的面积最少.
【解析】设鱼塘的长为xm,宽为ym,农田面积为s,则农田长为(x+6)m,宽为(y+6)m,xy=32400,s=(x+6)(y+6)=xy+6(x+y)+36,再由基本不等式即可得到所求最小值,及对应的x,y的值.
【考点精析】本题主要考查了基本不等式在最值问题中的应用的相关知识点,需要掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”才能正确解答此题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .任取t∈R,若函数f(x)在区间[t,t+1]上的最大值为M(t),最小值为m(t),记g(t)=M(t)﹣m(t).
.任取t∈R,若函数f(x)在区间[t,t+1]上的最大值为M(t),最小值为m(t),记g(t)=M(t)﹣m(t).
(1)求函数f(x)的最小正周期及对称轴方程;
(2)当t∈[﹣2,0]时,求函数g(t)的解析式;
(3)设函数h(x)=2|x﹣k|,H(x)=x|x﹣k|+2k﹣8,其中实数k为参数,且满足关于t的不等式 ![]() 有解,若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得h(x2)=H(x1)成立,求实数k的取值范围.
有解,若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得h(x2)=H(x1)成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C的坐标分别为(﹣ ![]() ,0),(
,0),( ![]() ,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.
,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心. 
(1)写出重心G的坐标;
(2)求外心O′,垂心H的坐标;
(3)求证:G,H,O′三点共线,且满足|GH|=2|OG′|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=SB,点M是SD的中点,AN⊥SC,且交SC于点N. 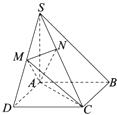
(1)求证:SC⊥平面AMN;
(2)求二面角D﹣AC﹣M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣2,0),B(2,0),P(x0 , y0)是直线y=x+3上任意一点,以A,B为焦点的椭圆过P,记椭圆离心率e关于x0的函数为e(x0),那么下列结论正确的是( )
A.e与x0一一对应
B.函数e(x0)无最小值,有最大值
C.函数e(x0)是增函数
D.函数e(x0)有最小值,无最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】与圆(x+1)2+y2=1和圆(x﹣5)2+y2=9都相切的圆的圆心轨迹是( )
A.椭圆和双曲线
B.两条双曲线
C.双曲线的两支
D.双曲线的一支
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把形如 ![]() 的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得 ![]() ,两边对x求导数,得
,两边对x求导数,得 ![]() ,于是
,于是 ![]() ,运用此方法可以求得函数
,运用此方法可以求得函数 ![]() 在(1,1)处的切线方程是 .
在(1,1)处的切线方程是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,则关于f(x)的说法正确的是( )
)的部分图象如图所示,则关于f(x)的说法正确的是( ) 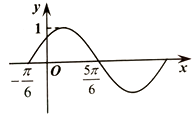
A.对称轴方程是x= ![]() +2kπ(k∈Z)
+2kπ(k∈Z)
B.φ=﹣ ![]()
C.最小正周期为π
D.在区间( ![]() ,
, ![]() )上单调递减
)上单调递减
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com