
【题目】已知![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数有两个极值点![]() 和
和![]() ,
,![]() 求证:b<2a
求证:b<2a
【答案】(1)(![]() ,1)是减区间,(0,
,1)是减区间,(0,![]() )和(1,+∞)是增区间;(2)详见解析
)和(1,+∞)是增区间;(2)详见解析
【解析】
试题分析:(1)将![]() 代入函数式,通过函数导数的正负得到函数的增减区间;(2)由题意可知
代入函数式,通过函数导数的正负得到函数的增减区间;(2)由题意可知![]() 是方程
是方程![]() 的根,依据根的分布规律可得
的根,依据根的分布规律可得![]() 的不等式,从而得到
的不等式,从而得到![]()
试题解析:(1)f‘(x)=2x-3+![]() =
=![]() (x>0), 2分
(x>0), 2分
由f'(x)=0得x=![]() 或x=1,.∴当x>1或0<x<
或x=1,.∴当x>1或0<x<![]() 时,f'(x)>0,
时,f'(x)>0,
当![]() <x<1时f'(x)<0, 4分
<x<1时f'(x)<0, 4分
∴(![]() ,1)是函数f(x)的减区间,(0,
,1)是函数f(x)的减区间,(0,![]() )和(1,+∞)是f(x)的增区间;..5分
)和(1,+∞)是f(x)的增区间;..5分
(2)∵函数f(x)有两个极值点x1,x2,∴f(x)=0在(0,+∞)有两个不同的解x1,x2,
.∵f(x)=ax+(b-1)+![]() =
=![]() , 6分
, 6分
∴x1,x2是ax2+(b-1)x+1=0在(0,+∞)内的两个不同解,
设h(x)=ax2+(b-1)x+1,则该函数有两个零点x1,x2,
∵0<x1<2<x2<4,∴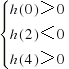 即
即![]() , 9分
, 9分
∴![]() -4a<b<
-4a<b<![]() -2a,即
-2a,即![]() -4a<
-4a<![]() -2a得a>
-2a得a>![]() , 11分
, 11分
∴b<![]() -2a<4a-2a=2a,∴b<2a得证;. 12分
-2a<4a-2a=2a,∴b<2a得证;. 12分


科目:高中数学 来源: 题型:
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且
且![]() 为等差数列
为等差数列![]() 的前三项.
的前三项.
(1)求![]() 与数列
与数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和
项和![]() ,试问是否存在正整数
,试问是否存在正整数![]() ,对任意的
,对任意的![]() 使得
使得![]() ?若存在请求出
?若存在请求出![]() 的最大值,若不存在请说明理由.
的最大值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是边长为
的底面是边长为![]() 的正方形,
的正方形, ![]() 底面
底面![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.
(Ⅰ)求证: ![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,试问在线段
,试问在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角 ![]() 的余弦值为
的余弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明当n∈N*时,1+2+22+…+25n-1是31的倍数时,当n=1时原式为( )
A. 1 B. 1+2
C. 1+2+3+4 D. 1+2+22+23+24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车公司为了考查某![]() 店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店或保养后可以对该店进行打分,最高分为10分.上个月公司对该
店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店或保养后可以对该店进行打分,最高分为10分.上个月公司对该![]() 店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:第一组
店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() a,第五组
a,第五组![]() ,得到频率分布直方图如图所示.
,得到频率分布直方图如图所示.
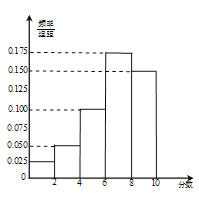
(1)求所打分值在![]() 的客户的人数;
的客户的人数;
(2)该公司在第二、三组客户中按分层抽样的方法抽取6名客户进行深入调查,之后将从这6人中随机抽取2人进行物质奖励,求得到奖励的人来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的四个顶点分别为
的四个顶点分别为![]() ,左右焦点分别为
,左右焦点分别为![]() ,若圆
,若圆![]() :
:![]() 上有且只有一个点
上有且只有一个点![]() 满足
满足![]() .
.
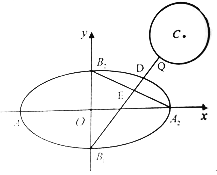
(1)求圆![]() 的半径
的半径![]() ;
;
(2)若点![]() 为圆
为圆![]() 上的一个动点,直线
上的一个动点,直线![]() 交椭圆于点
交椭圆于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com