
【题目】等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P﹣AE﹣C为120°,设点P在面ABE上的射影为H. 
(1)证明:点H为EB的中点;
(2)若 ![]() ,求直线BE与平面ABP所成角的正弦值.
,求直线BE与平面ABP所成角的正弦值.
【答案】
(1)证明:依题意,AE⊥BC,则AE⊥EB,AE⊥EP,EB∩EP=E.
∴AE⊥面EPB.
故∠CEP为二面角C﹣AE﹣P的平面角,则点P在面ABE上的射影H在EB上.
由∠CEP=120°得∠PEB=60°.
∴EH= ![]() EP=
EP= ![]() .
.
∴H为EB的中点.
(2)解:过H作HM⊥AB于M,连PM,过H作HN⊥PM于N,连BN,
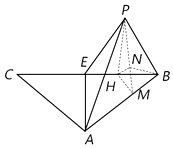
则有三垂线定理得AB⊥面PHM.即面PHM⊥面PAB,
∴HN⊥面PAB.故HB在面PAB上的射影为NB.
∴∠HBN为直线BE与面ABP所成的角.
依题意,BE= ![]() BC=2,BH=
BC=2,BH= ![]() BE=1.
BE=1.
在△HMB中,HM= ![]() ,
,
在△EPB中,PH= ![]() ,
,
∴在Rt△PHM中,HN= ![]() .
.
∴sin∠HBN= ![]() .
.
【解析】(1)证明:∠CEP为二面角C﹣AE﹣P的平面角,则点P在面ABE上的射影H在EB上,即可证明点H为EB的中点;(2)过H作HM⊥AB于M,连PM,过H作HN⊥PM于N,连BN,则有三垂线定理得AB⊥面PHM.即面PHM⊥面PAB,HN⊥面PAB.故HB在面PAB上的射影为NB,∠HBN为直线BE与面ABP所成的角,即可求直线BE与平面ABP所成角的正弦值.
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则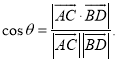 .
.


科目:高中数学 来源: 题型:
【题目】设Sn , Tn分别是数列{an},{bn}的前n项和,已知对于任意n∈N* , 都有3an=2Sn+3,数列{bn}是等差数列,且T5=25,b10=19. (Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn= ![]() ,求数列{cn}的前n项和Rn , 并求Rn的最小值.
,求数列{cn}的前n项和Rn , 并求Rn的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式|x﹣2|﹣|x+3|≥|m+1|有解,记实数m的最大值为M.
(1)求M的值;
(2)正数a,b,c满足a+2b+c=M,求证: ![]() +
+ ![]() ≥1.
≥1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】G为△ADE的重心,点P为△DEG内部(含边界)上任一点,B,C均为AD,AE上的三等分点(靠近点A), ![]() =α
=α ![]() +β
+β ![]() (α,β∈R),则α+
(α,β∈R),则α+ ![]() β的范围是( )
β的范围是( )
A.[1,2]
B.[1, ![]() ]
]
C.[ ![]() ,2]
,2]
D.[ ![]() ,3]
,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由正数组成的等比数列{an}中,公比q="2," a1·a2·a3·…·a30=245, 则a1·a4·a7·…·a28= ( )
A.25
B.210
C.215
D.220
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村投资128万元建起了一处生态采摘园,预计在经营过程中,第一年支出10万元,以后每年支出都比上一年增加4万元,从第一年起每年的销售收入都为76万元.设y表示前n(n∈N*)年的纯利润总和(利润总和=经营总收入﹣经营总支出﹣投资).
(1)该生态园从第几年开始盈利?
(2)该生态园前几年的年平均利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+ ![]() x2在x=﹣1处取得极大值,记g(x)=
x2在x=﹣1处取得极大值,记g(x)= ![]() .程序框图如图所示,若输出的结果S>
.程序框图如图所示,若输出的结果S> ![]() ,则判断框中可以填入的关于n的判断条件是( )
,则判断框中可以填入的关于n的判断条件是( ) 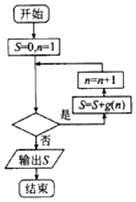
A.n≤2014?
B.n≤2015?
C.n>2014?
D.n>2015?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com