
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,cosB=![]() .
.
(Ⅰ)若c=2a,求![]() 的值;
的值;
(Ⅱ)若C-B=![]() ,求sinA的值.
,求sinA的值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由余弦定理结合![]() ;可得
;可得![]() ,再由正弦定理可得结果;(2)先由
,再由正弦定理可得结果;(2)先由![]() ,根据二倍角公式可得
,根据二倍角公式可得![]() ,则
,则![]() ,根据两角差的正弦公式可得结果.
,根据两角差的正弦公式可得结果.
试题解析:(1)解法1
在△ABC中,因为cosB=![]() ,所以
,所以![]() =
=![]() .
.
因为c=2a,所以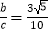 =
=![]() ,即
,即![]() =
=![]() ,
,
所以![]() =
=![]() .
.
又由正弦定理得![]() =
=![]() ,
,
所以![]() =
=![]() .
.
解法2
因为cosB=![]() ,B∈(0,),所以sinB=
,B∈(0,),所以sinB=![]() =
=![]() .
.
因为c=2a,由正弦定理得sinC=2sinA,
所以sinC=2sin(B+C)=![]() cosC+
cosC+![]() sinC,
sinC,
即-sinC=2cosC.
又因为sin2C+cos2C=1,sinC>0,解得sinC=![]() ,
,
所以![]() =
=![]() .
.
(2)因为cosB=![]() ,所以cos2B=2cos2B-1=
,所以cos2B=2cos2B-1=![]() .
.
又0<B<π,所以sinB=![]() =
=![]() ,
,
所以sin2B=2sinBcosB=2×![]() ×
×![]() =
=![]() .
.
因为C-B=![]() ,即C=B+
,即C=B+![]() ,所以A=π-(B+C)=
,所以A=π-(B+C)=![]() -2B,
-2B,
所以sinA=sin(![]() -2B)
-2B)
=sin![]() cos2B-cos
cos2B-cos![]() sin2B
sin2B
=![]() ×
×![]() -(-
-(-![]() )×
)×![]()
=![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,侧面
中,侧面![]() 是边长为
是边长为![]() 的正三角形,
的正三角形,![]() ,平面
,平面![]() 平面
平面![]() ,把平面
,把平面![]() 沿
沿![]() 旋转至平面
旋转至平面![]() 的位置,记点
的位置,记点![]() 旋转后对应的点为
旋转后对应的点为![]() (不在平面
(不在平面![]() 内),
内),![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
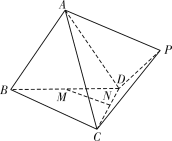
(1)求证:![]() ;
;
(2)求三棱锥![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1(﹣c,0),F2(c,0)分别为双曲线C:![]() 1(a>0,b>0)的左、右焦点,直线l:
1(a>0,b>0)的左、右焦点,直线l:![]() 1与C交于M,N两点,线段MN的垂直平分线与x轴交于T(﹣5c,0),则C的离心率为( )
1与C交于M,N两点,线段MN的垂直平分线与x轴交于T(﹣5c,0),则C的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|x+2|+|x﹣3|.
(1)求不等式f(x)≥8的解集;
(2)若a>0,b>0,且函数F(x)=f(x)﹣3a﹣2b有唯一零点x0,证明:![]() f(x0).
f(x0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是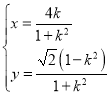 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒肺炎正在全球蔓延,对世界经济影响严重,中国疫情防控,复工复学恢复经济成为各国的榜样,绵阳某商场在五一劳动节期间举行促销活动,根据市场调查,该商场决定从3种服装商品、2种家电、4种日用商品中,选出3种商品进行促销活动.
(1)试求选出的3种商品至少有2种服装商品的概率;
(2)商场对选的A商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高300元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金,假设顾客每次抽奖时获奖与否是等概率的,请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是
是![]() 与
与![]() 的一个交点,其极坐标为
的一个交点,其极坐标为![]() .设射线
.设射线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com