
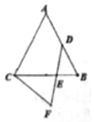
 如图,△ABC为边长为1的正三角形,D为AB的中点,E在BC上,且BE:EC=1:2,连结DE并延长至F,使EF=DE,连结FC,则$\overrightarrow{FC}$•$\overrightarrow{AC}$的值为$\frac{7}{12}$.
如图,△ABC为边长为1的正三角形,D为AB的中点,E在BC上,且BE:EC=1:2,连结DE并延长至F,使EF=DE,连结FC,则$\overrightarrow{FC}$•$\overrightarrow{AC}$的值为$\frac{7}{12}$. 分析 建立平面直角坐标系,转化为坐标运算即可.
解答 解:如图建立平面直角坐标系,依题意得A(0,0),B($\frac{1}{2}$$\frac{\sqrt{3}}{2}$),C(1,0),
∵D为AB的中点,E在BC上,且BE:EC=1:2,∴D($\frac{1}{4},\frac{\sqrt{3}}{4}$),E($\frac{1}{3}$,0)
∵EF=DE∴F($\frac{5}{12}$,-$\frac{\sqrt{3}}{4}$)
$\overrightarrow{FC}=(\frac{7}{12},\frac{\sqrt{3}}{4})$,$\overrightarrow{AC}=(1,0)$
则$\overrightarrow{FC}$•$\overrightarrow{AC}$=$\frac{7}{12}×1+\frac{\sqrt{3}}{4}×0=\frac{7}{12}$,
故答案为:$\frac{7}{12}$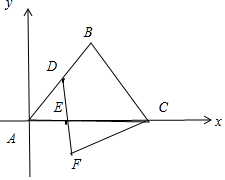
点评 本题考查平面向量基本定理、数量积运算性质,建立坐标系转化为坐标运算是关键,属于基础题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=2x | B. | f(x)=log${\;}_{\frac{1}{2}}$x | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=-x|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,16} | B. | {0,1} | C. | {1,16} | D. | {0,1,4,16} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | $({\frac{3}{4},+∞})$ | C. | (0,2) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,8) | C. | (4,8) | D. | [4,8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com