
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (其中t为参数,
(其中t为参数,![]() ).在以原点O为极点,x轴的非负半轴为极轴所建立的极坐标系中,曲线C的极坐标方程为
).在以原点O为极点,x轴的非负半轴为极轴所建立的极坐标系中,曲线C的极坐标方程为![]() .设直线l与曲线C相交于A,B两点.
.设直线l与曲线C相交于A,B两点.
(1)求曲线C和直线l的直角坐标方程;
(2)已知点![]() ,求
,求![]() 的最大值.
的最大值.
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】已知三个不同平面![]() 、
、![]() 、
、![]() 和直线
和直线![]() ,下面有四个命题:
,下面有四个命题:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②直线![]() 上有两点到平面
上有两点到平面![]() 的距离相等,则
的距离相等,则![]() ;
;
③![]() ,
,![]() ,则
,则![]() ;
;
④若直线![]() 不在平面
不在平面![]() 内,
内,![]() ,
,![]() ,则
,则![]() .
.
则正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
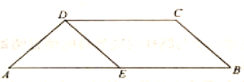
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
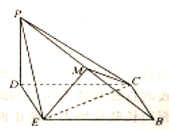
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】开学后,某学校食堂为了减少师生就餐排队时间,特推出即点即取的米饭套餐和面食套餐两种,已知小明同学每天中午都会在食堂提供的米饭套餐和面食套餐中选择一种,米饭套餐的价格是每份15元,面食套餐的价格是每份10元,如果小明当天选择了某种套餐,她第二天会有![]() 的可能性换另一种类型的套餐,假如第1天小明选择了米饭套餐,第n天选择米饭套餐的概率
的可能性换另一种类型的套餐,假如第1天小明选择了米饭套餐,第n天选择米饭套餐的概率![]() ,给出以下论述:①小明同学第二天一定选择面食套餐;②
,给出以下论述:①小明同学第二天一定选择面食套餐;②![]() ;③
;③![]() ;④前n天小明同学午餐花费的总费用数学期望为
;④前n天小明同学午餐花费的总费用数学期望为![]() .其中正确的是( )
.其中正确的是( )
A.②④B.①②③C.③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,离心率
,离心率![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,圆
为原点,圆![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一动点,若直线
上一动点,若直线![]() 、
、![]() 与
与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为2的![]() 切直线MN于点P,射线PK从PN出发绕点P逆时针方向旋转到PM,旋转过程中,PK交
切直线MN于点P,射线PK从PN出发绕点P逆时针方向旋转到PM,旋转过程中,PK交![]() 于点Q,设
于点Q,设![]() 为x,弓形PmQ的面积为
为x,弓形PmQ的面积为![]() ,那么
,那么![]() 的图象大致是
的图象大致是![]()
![]()

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com