
分析 (1)求出F(0,1),得到抛物线方程,联立圆的方程与抛物线方程,求出A的纵坐标,然后求解|AF|.
(2)设M(x0,y0),求出切线l:y=$\frac{{x}_{0}}{p}$(x-x0)+y0,通过|ON|=1,求出p=$\frac{2{y}_{0}}{{{y}_{0}}^{2}-1}$且${{y}_{0}}^{2}$-1>0,求出|MN|2的表达式,利用基本不等式求解最小值以及p的值即可.
解答 解:(1)由题意得F(0,1),从而有C:x2=4y.
解方程组$\left\{\begin{array}{l}{{x}^{2}=4y}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,得yA=$\sqrt{5}$-2,所以|AF|=$\sqrt{5}$-1.…(5分)
(2)设M(x0,y0),则切线l:y=$\frac{x0}{p}$(x-x0)+y0,
整理得x0x-py-py0=0.…(6分)
由|ON|=1得|py0|=$\sqrt{{{x}_{0}}^{2}+{p}^{2}}$=$\sqrt{2p{y}_{0}+{p}^{2}}$,
所以p=$\frac{2{y}_{0}}{{{y}_{0}}^{2}-1}$且${{y}_{0}}^{2}$-1>0,…(8分)
所以|MN|2=|OM|2-1=${{x}_{0}}^{2}$+${{y}_{0}}^{2}$-1=2py0+${{y}_{0}}^{2}$-1
=$\frac{4{{y}_{0}}^{2}}{{{y}_{0}}^{2}-1}$+${{y}_{0}}^{2}$-1=4+$\frac{4}{{{y}_{0}}^{2}-1}$+(${{y}_{0}}^{2}$-1)≥8,当且仅当y0=$\sqrt{3}$时等号成立,
所以|MN|的最小值为2$\sqrt{2}$,此时p=$\sqrt{3}$.…(12分)
点评 本题考查直线与抛物线的位置关系的应用,抛物线方程的求法,抛物线与圆的位置关系的应用,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2017}$,+∞) | B. | (-2017,+∞) | C. | (-$\frac{2}{3}$,+∞) | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{5}$] | B. | [-$\frac{1}{5}$,1] | C. | (-$\frac{1}{5}$,$\frac{1}{3}$] | D. | ($\frac{1}{3}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
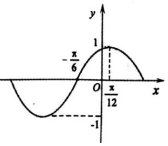 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2${\;}^{(1-kt)(x-b)^{2}}$,(其中,t为关税的税率,且t∈[0,$\frac{1}{2}$),x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时的市场供应量曲线如图.
据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2${\;}^{(1-kt)(x-b)^{2}}$,(其中,t为关税的税率,且t∈[0,$\frac{1}{2}$),x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时的市场供应量曲线如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com