
| A. | -3 | B. | 3 | C. | -8 | D. | 8 |
分析 利用偶函数f(x)在区间(-∞,0)上是单调函数,从而$f(x)=f(\frac{x+2}{x+4})$等价于x=$\frac{x+2}{x+4}$或-x=$\frac{x+2}{x+4}$,由此即可得出结论.
解答 解:∵偶函数f(x)在区间(-∞,0)上是单调函数,
∴$f(x)=f(\frac{x+2}{x+4})$等价于x=$\frac{x+2}{x+4}$或-x=$\frac{x+2}{x+4}$
∴x2+3x-2=0或x2+5x+2=0,
此时x1+x2=-3或x3+x4=-5.
∴满足$f(x)=f(\frac{x+2}{x+4})$的所有x之和为-3-5=-8.
故选C.
点评 本题考查函数性质的综合应用,考查学生分析解决问题的能力,属于中档题.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
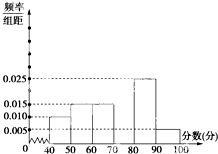 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | X=Y$\underset{?}{≠}$Z | B. | X$\underset{?}{≠}$Y=Z | C. | X$\underset{?}{≠}$Y$\underset{?}{≠}$Z | D. | X$\underset{?}{≠}$Z$\underset{?}{≠}$Y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:2 | B. | 2:3 | C. | 3:7 | D. | 7:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0] | B. | (-3,0) | C. | [-3,0] | D. | [-3,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | (0,0.25] | (0.25,0.50] | (0.50,0.75] | (0.75,1] | (1,1.25] | (1.25,1.5] |
| 数据 | 6 | 4 | 3 | 2 | 2 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com