
| A.25元 | B.20.5元 | C.15元 | D.12.5元 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 万件,则需另投入成本
万件,则需另投入成本 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时, ;A产品年产量大于80万件时,
;A产品年产量大于80万件时, 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。 的函数解析式
的函数解析式 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 万件,需另投入的成本为
万件,需另投入的成本为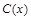 (单位:万元),当年产量小于80万件时,
(单位:万元),当年产量小于80万件时, ;当年产量不小于80万件时,
;当年产量不小于80万件时, .假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
.假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完. (万元)关于年产量
(万元)关于年产量 (万件)的函数关系式;
(万件)的函数关系式;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.49 h | B.56 h | C.64 h | D.72 h |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.上午10:00 | B.中午12:00 |
| C.下午4:00 | D.下午6:00 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.f(5)=1 |
B.方程f(x)= 有且仅有一个解 有且仅有一个解 |
| C.函数f(x)是周期函数 |
| D.函数f(x)是减函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,分别求f1(x)和f2(x);
,分别求f1(x)和f2(x);查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
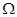 为平面直角坐标系
为平面直角坐标系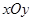 中的点集,从
中的点集,从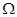 中的任意一点
中的任意一点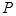 作
作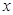 轴、
轴、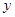 轴的垂线,垂足分别为
轴的垂线,垂足分别为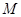 ,
,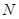 ,记点
,记点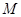 的横坐标的最大值与最小值之差为
的横坐标的最大值与最小值之差为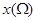 ,点
,点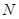 的纵坐标的最大值与最小值之差为
的纵坐标的最大值与最小值之差为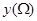 . 若
. 若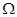 是边长为1的正方形,给出下列三个结论:
是边长为1的正方形,给出下列三个结论: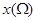 的最大值为
的最大值为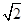 ;
;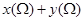 的取值范围是
的取值范围是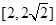 ;
;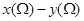 恒等于0.其中所有正确结论的序号是( )
恒等于0.其中所有正确结论的序号是( )| A.① | B.②③ | C.①② | D.①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com