
【题目】已知函数f(x)=x2+2ax+2,x∈[﹣5,5].
(1)求实数a的范围,使y=f(x)在区间[﹣5,5]上是单调函数.
(2)求f(x)的最小值.
【答案】
(1)解:因为f(x)是开口向上的二次函数,且对称轴为x=﹣a,
为了使f(x)在[﹣5,5]上是单调函数,故﹣a≤﹣5或﹣a≥5,即a≥5或a≤﹣5
(2)解:①当﹣a≤﹣5,即a≥5时,f(x)在[﹣5,5]上是增函数,
所以fmin(x)=f(﹣5)=27﹣10a
②当﹣5<﹣a≤5,即﹣5≤a<5时,f(x)在[﹣5,﹣a]上是减函数,在[﹣a,5]上是增函数,
所以 ![]()
③当﹣a>5,即a<﹣5时,f(x)在[﹣5,5]上是减函数,
所以fmin(x)=f(5)=27+10a
综上可得 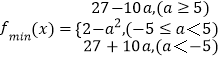
【解析】(1)由题意,得函数y=f(x)的单调区间是(﹣∞,﹣a],[﹣a,+∞),
由于y=f(x)在区间[﹣5,5]上是单调函数故﹣a≤﹣5或﹣a≥5,即可得到实数a的取值范围;(2)分类讨论,得到函数在[﹣5,5]上的增减性,继而得到函数在[﹣5,5]上的最小值.
【考点精析】本题主要考查了二次函数在闭区间上的最值的相关知识点,需要掌握当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() 才能正确解答此题.
才能正确解答此题.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】若不等式(1-a)x2-4x+6>0的解集是{x|-3<x<1}.
(1)解不等式2x2+(2-a)x-a>0;
(2)b为何值时,ax2+bx+3≥0的解集为R.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l与圆C:x2+y2+2x﹣4y+a=0相交于A,B两点,弦AB的中点为M(0,1).
(1)若圆C的半径为![]() ,求实数a的值;
,求实数a的值;
(2)若弦AB的长为6,求实数a的值;
(3)当a=1时,圆O:x2+y2=2与圆C交于M,N两点,求弦MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线y2=2px(p>0)的焦点,斜率为2![]() 的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
(1)求该抛物线的方程.
(2)O为坐标原点,C为抛物线上一点,若![]() ,求λ的值
,求λ的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线l:y=2x上,且经过点A(﹣3,﹣1),B(4,6).
(Ⅰ)求圆C的方程;
(Ⅱ)点P是直线l上横坐标为﹣4的点,过点P作圆C的切线,求切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(﹣∞,+∞)上的偶函数,且在(﹣∞,0]上是增函数,设a=f(log47),b=f(log ![]() 3),c=f(21.6),则a,b,c的大小关系是( )
3),c=f(21.6),则a,b,c的大小关系是( )
A.c<a<b
B.c<b<a
C.b<c<a
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年9月16日05时,第19号台风“杜苏芮”的中心位于甲地,它以每小时30千米的速度向西偏北![]() 的方向移动,距台风中心
的方向移动,距台风中心![]() 千米以内的地区都将受到影响,若16日08时到17日08时,距甲地正西方向900千米的乙地恰好受台风影响,则
千米以内的地区都将受到影响,若16日08时到17日08时,距甲地正西方向900千米的乙地恰好受台风影响,则![]() 和
和![]() 的值分别为(附:
的值分别为(附: ![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com