
ЁОЬтФПЁПМЭФюБвЪЧвЛИіЙњМвЮЊМЭФюЙњМЪЛђБОЙњЕФеўжЮЁЂРњЪЗЃЌЮФЛЏЕШЗНУцЕФжиДѓЪТМўЁЂНмГіШЫЮяЁЂУћЪЄЙХМЃЁЂефЯЁЖЏжВЮяЁЂЬхг§ШќЪТЕШЖјЗЂааЕФЗЈЖЈЛѕБв.ЮвЙњдк1984ФъЪзДЮЗЂааМЭФюБвЃЌФПЧАвбЗЂааСЫ115ЬзМЭФюБвЃЌетаЉМЭФюБвЩюЪмгЪБвАЎКУепЕФЯВАЎгыЪеВи.2019ФъЗЂааЕФЕк115ЬзМЭФюБвЁАЫЋвХВњжЎЬЉЩНБвЁБЪЧФПЧАЮЊжЙЗЂааЕФЕквЛЬзвьаЮБвЃЌвђЮЊетЬзМЭФюБвЕФЖржжЬижЪЃЌИќМгЪмЕНАЎКУепзЗХѕ.ФГЛњЙЙЮЊЕїВщЮвЙњЙЋУёЖдМЭФюБвЕФЯВАЎЬЌЖШЃЌЫцЛњбЁСЫФГГЧЪаФГаЁЧјЕФ50ЮЛОгУёЕїВщЃЌЕїВщНсЙћЭГМЦШчЯТЃК
ЯВАЎ | ВЛЯВАЎ | КЯМЦ | |
ФъСфВЛДѓгк40Ыъ | 24 | ||
ФъСфДѓгк40Ыъ | 20 | ||
КЯМЦ | 22 | 50 |
ЃЈ1ЃЉИљОнвбгаЪ§ОнЃЌАбБэИёЪ§ОнЬюаДЭъећЃЌХаЖЯФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЧАЬсЯТШЯЮЊВЛЭЌФъСфгыМЭФюБвЕФЯВАЎЮоЙиЃП
ЕФЧАЬсЯТШЯЮЊВЛЭЌФъСфгыМЭФюБвЕФЯВАЎЮоЙиЃП
ЃЈ2ЃЉвбжЊдкБЛЕїВщЕФФъСфВЛДѓгк40ЫъЕФЯВАЎепжага5УћФаадЃЌЦфжа3ЮЛЪЧбЇЩњЃЌЯжДгет5УћФааджаЫцЛњГщШЁ2ШЫЃЌЧѓжСЖрга1ЮЛбЇЩњЕФИХТЪ.
ИНЃК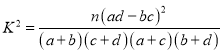 ЃЌ
ЃЌ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
ЁОД№АИЁПЃЈ1ЃЉБэМћНтЮіЃЌЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЬѕМўЯТШЯЮЊВЛЭЌФъСфгыМЭФюБвЕФЯВАЎЮоЙиЃЛЃЈ2ЃЉ
ЕФЬѕМўЯТШЯЮЊВЛЭЌФъСфгыМЭФюБвЕФЯВАЎЮоЙиЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬѕМўЃЌСаГіСаСЊБэЃЌЬюЩЯЖдгІЕФЪ§ОнЃЌАбЧѓЕУЕФЪ§ОнДњШыЧѓ![]() ЕФЙЋЪНЧѓГіжЕЃЌВЂХаЖЯМДПЩЕУЕННсТлЃЛ
ЕФЙЋЪНЧѓГіжЕЃЌВЂХаЖЯМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉРћгУСаОйЗЈШЗЖЈЛљБОЪТМўЃЌМДПЩЧѓГіИХТЪ.
ЯВАЎ | ВЛЯВАЎ | КЯМЦ | |
ФъСфВЛДѓгк40Ыъ | 8 | 16 | 24 |
ФъСфДѓгк40Ыъ | 20 | 6 | 26 |
КЯМЦ | 28 | 22 | 50 |
ЃЈ1ЃЉ![]()
![]() .
.
ЁрФмдкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЬѕМўЯТШЯЮЊВЛЭЌФъСфгыМЭФюБвЕФЯВАЎЮоЙи.
ЕФЬѕМўЯТШЯЮЊВЛЭЌФъСфгыМЭФюБвЕФЯВАЎЮоЙи.
ЃЈ2ЃЉМЧВЛДѓгк40ЫъЕФ5ЮЛЯВАЎепжаЕФ3ЮЛбЇЩњМЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЗЧбЇЩњМЧЮЊ
ЃЌЗЧбЇЩњМЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дђДг5ШЫжаШЮШЁ2ШЫЃЌЙВга![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЙВ10жжНсЙћ.
ЙВ10жжНсЙћ.
ЦфжажСЖрга1ЮЛбЇЩњЕФга7жжЃЌЁржСЖрга1ЮЛбЇЩњЕФИХТЪ![]() .
.


 ЛЦИдКЃЕэШЋГЬХргХВтЪдОэЯЕСаД№АИ
ЛЦИдКЃЕэШЋГЬХргХВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧњЯп![]() ЩЯЖЏЕу
ЩЯЖЏЕу![]() ЕНЖЈЕу
ЕНЖЈЕу![]() гыЖЈжБЯп
гыЖЈжБЯп![]() ЕФОрРыжЎБШЮЊГЃЪ§
ЕФОрРыжЎБШЮЊГЃЪ§![]() ЃЛ
ЃЛ
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЙьМЃЗНГЬЃЛ
ЕФЙьМЃЗНГЬЃЛ
ЃЈ2ЃЉЩшдВаФЮЊ![]() ЕФдВ
ЕФдВ![]()
![]() гыЧњЯп
гыЧњЯп![]() НЛгкЕу
НЛгкЕу![]() гыЕу
гыЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЌВЂЧѓДЫЪБдВ
ЕФзюаЁжЕЃЌВЂЧѓДЫЪБдВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§РтзЖ![]() жаЃЌЦНУц
жаЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ОљЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ОљЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЕФжаЕу.
ЕФжаЕу.
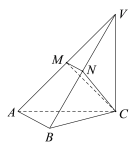
ЃЈЂёЃЉЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈЂђЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈЂѓЃЉЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=AsinЃЈІиx+ІеЃЉЃЈAЃО0ЃЌІиЃО0ЃЌ|Іе|ЃМ![]() ЃЉЕФВПЗжЭМЯѓШчЭМЫљЪО.
ЃЉЕФВПЗжЭМЯѓШчЭМЫљЪО.
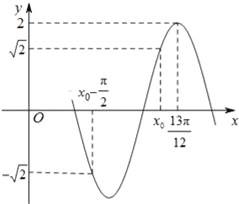
ЃЈЂёЃЉаДГіКЏЪ§fЃЈxЃЉЕФНтЮіЪНМАx0ЕФжЕЃЛ
ЃЈЂђЃЉЧѓКЏЪ§fЃЈxЃЉдкЧјМф[Љ![]() ЃЌ
ЃЌ![]() ]ЩЯЕФзюДѓжЕгызюаЁжЕ.
]ЩЯЕФзюДѓжЕгызюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() ЪЧЖЈвхдк
ЪЧЖЈвхдк![]() ЩЯЕФЦцКЏЪ§ЃЌЖд
ЩЯЕФЦцКЏЪ§ЃЌЖд![]() ЃЌОљга
ЃЌОљга![]() ЃЌвбжЊЕБ
ЃЌвбжЊЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌдђЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
ЃЌдђЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
A. ![]() ЕФЭМЯѓЙигк
ЕФЭМЯѓЙигк![]() ЖдГЦ B.
ЖдГЦ B. ![]() газюДѓжЕ1
газюДѓжЕ1
C. ![]() дк
дк![]() ЩЯга5ИіСуЕу D. ЕБ
ЩЯга5ИіСуЕу D. ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() .
.
(1)Шє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
(2)ШєЕБ![]() ЪБ
ЪБ![]() КуГЩСЂЃЌЧѓ
КуГЩСЂЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌШчЙћДцдкИјЖЈЕФЪЕЪ§Жд
ЃЌШчЙћДцдкИјЖЈЕФЪЕЪ§Жд![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() КуГЩСЂЃЌдђГЦ
КуГЩСЂЃЌдђГЦ![]() ЮЊЁА
ЮЊЁА![]() КЏЪ§ЁБЃЛ
КЏЪ§ЁБЃЛ
ЃЈ1ЃЉХаЖЯКЏЪ§![]() ЃЌ
ЃЌ![]() ЪЧЗёЪЧЁА
ЪЧЗёЪЧЁА![]() КЏЪ§ЁБЃЛ
КЏЪ§ЁБЃЛ
ЃЈ2ЃЉШє![]() ЪЧвЛИіЁА
ЪЧвЛИіЁА![]() КЏЪ§ЁБЃЌЧѓГіЫљгаТњзуЬѕМўЕФгаађЪЕЪ§Жд
КЏЪ§ЁБЃЌЧѓГіЫљгаТњзуЬѕМўЕФгаађЪЕЪ§Жд![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєЖЈвхгђЮЊ![]() ЕФКЏЪ§
ЕФКЏЪ§![]() ЪЧЁА
ЪЧЁА![]() КЏЪ§ЁБЃЌЧвДцдкТњзуЬѕМўЕФгаађЪЕЪ§Жд
КЏЪ§ЁБЃЌЧвДцдкТњзуЬѕМўЕФгаађЪЕЪ§Жд![]() КЭ
КЭ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕгђЮЊ
ЕФжЕгђЮЊ![]() ЃЌЧѓЕБ
ЃЌЧѓЕБ![]() ЪБ
ЪБ![]() ЕФжЕгђЃЛ
ЕФжЕгђЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЪЧдВ
ЪЧдВ![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЃЌ
ЃЌ![]() дкдВЩЯЧвЗжБ№дк
дкдВЩЯЧвЗжБ№дк![]() ЕФСНВрЃЌЦфжа
ЕФСНВрЃЌЦфжа![]() ЃЌ
ЃЌ![]() .ЯжНЋЦфби
.ЯжНЋЦфби![]() елЦ№ЪЙЕУЖўУцНЧ
елЦ№ЪЙЕУЖўУцНЧ![]() ЮЊжБЖўУцНЧЃЌдђЯТСаЫЕЗЈВЛе§ШЗЕФЪЧЃЈ ЃЉ
ЮЊжБЖўУцНЧЃЌдђЯТСаЫЕЗЈВЛе§ШЗЕФЪЧЃЈ ЃЉ
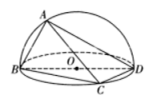
A.![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() дкЭЌвЛИіЧђУцЩЯ
дкЭЌвЛИіЧђУцЩЯ
B.ЕБ![]() ЪБЃЌШ§РтзЖ
ЪБЃЌШ§РтзЖ![]() ЕФЬхЛ§ЮЊ
ЕФЬхЛ§ЮЊ![]()
C.![]() гы
гы![]() ЪЧвьУцжБЯпЧвВЛДЙжБ
ЪЧвьУцжБЯпЧвВЛДЙжБ
D.ДцдквЛИіЮЛжУЃЌЪЙЕУЦНУц![]() ЦНУц
ЦНУц![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЙсГЙжаЙВжабыЁЂЙњЮёдКЙигкОЋзМЗіЦЖеўВпЕФЙ§ГЬжаЃЌФГЕЅЮЛдкФГЪаЖЈЕуАяЗіФГДх![]() ЛЇЦЖРЇЛЇ.ЮЊСЫзіЕНОЋзМАяЗіЃЌЙЄзїзщЖдет
ЛЇЦЖРЇЛЇ.ЮЊСЫзіЕНОЋзМАяЗіЃЌЙЄзїзщЖдет![]() ЛЇДхУёЕФФъЪеШыЧщПіЁЂЮЃОЩЗПЧщПіЁЂЛМВЁЧщПіЕШНјааЕїВщЃЌВЂАбЕїВщНсЙћзЊЛЏЮЊИїЛЇЕФЦЖРЇжИБъ
ЛЇДхУёЕФФъЪеШыЧщПіЁЂЮЃОЩЗПЧщПіЁЂЛМВЁЧщПіЕШНјааЕїВщЃЌВЂАбЕїВщНсЙћзЊЛЏЮЊИїЛЇЕФЦЖРЇжИБъ![]() .НЋжИБъ
.НЋжИБъ![]() АДее
АДее![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЗжГЩЮхзщЃЌЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМ.ЙцЖЈШє
ЗжГЩЮхзщЃЌЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМ.ЙцЖЈШє![]() ЃЌдђШЯЖЈИУЛЇЮЊЁАОјЖдЦЖРЇЛЇЁБЃЌЗёдђШЯЖЈИУЛЇЮЊЁАЯрЖдЦЖРЇЛЇЁБЃЛЕБ
ЃЌдђШЯЖЈИУЛЇЮЊЁАОјЖдЦЖРЇЛЇЁБЃЌЗёдђШЯЖЈИУЛЇЮЊЁАЯрЖдЦЖРЇЛЇЁБЃЛЕБ![]() ЪБЃЌШЯЖЈИУЛЇЮЊЁАиНД§АязЁЛЇЁБ.ЙЄзїзщгжЖдет
ЪБЃЌШЯЖЈИУЛЇЮЊЁАиНД§АязЁЛЇЁБ.ЙЄзїзщгжЖдет![]() ЛЇМвЭЅЕФЪмНЬг§ЫЎЦННјааЦРВтЃЌМвЭЅЪмНЬг§ЫЎЦНМЧЮЊЁАСМКУЁБгыЁАВЛКУЁБСНжж.
ЛЇМвЭЅЕФЪмНЬг§ЫЎЦННјааЦРВтЃЌМвЭЅЪмНЬг§ЫЎЦНМЧЮЊЁАСМКУЁБгыЁАВЛКУЁБСНжж.

ЃЈ1ЃЉЭъГЩЯТУцЕФСаСЊБэЃЌВЂХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊОјЖдЦЖРЇЛЇЪ§гыЪмНЬг§ЫЎЦНВЛКУгаЙиЃК
ЕФАбЮеШЯЮЊОјЖдЦЖРЇЛЇЪ§гыЪмНЬг§ЫЎЦНВЛКУгаЙиЃК
ЪмНЬг§ЫЎЦНСМКУ | ЪмНЬг§ЫЎЦНВЛКУ | змМЦ | |
ОјЖдЦЖРЇЛЇ |
| ||
ЯрЖдЦЖРЇЛЇ |
| ||
змМЦ |
|
ЃЈ2ЃЉЩЯМЖВПУХЮЊСЫЕїВщетИіДхЕФЬиРЇЛЇЗжВМЧщПіЃЌдкЦЖРЇжИБъДІгк![]() ЕФЦЖРЇЛЇжаЃЌЫцЛњбЁШЁСНЛЇЃЌгУ
ЕФЦЖРЇЛЇжаЃЌЫцЛњбЁШЁСНЛЇЃЌгУ![]() БэЪОЫљбЁСНЛЇжаЁАиНД§АяжњЛЇЁБЕФЛЇЪ§ЃЌЧѓ
БэЪОЫљбЁСНЛЇжаЁАиНД§АяжњЛЇЁБЕФЛЇЪ§ЃЌЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ
ЕФЗжВМСаКЭЪ§бЇЦкЭћ![]() .
.
ИНЃК ЃЌЦфжа
ЃЌЦфжа![]() .
.
|
|
|
|
|
|
|
|
|
|
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com